题目内容
4.若a>0,b>0,且$\sqrt{a}$($\sqrt{a}$-2$\sqrt{b}$)=5$\sqrt{b}$($\sqrt{a}$+6$\sqrt{b}$),求$\frac{4a+\sqrt{ab}+4b}{2a+\sqrt{ab}-3b}$的值.分析 先把$\sqrt{a}$($\sqrt{a}$-2$\sqrt{b}$)=5$\sqrt{b}$($\sqrt{a}$+6$\sqrt{b}$)转化为($\sqrt{a}$-10$\sqrt{b}$)($\sqrt{a}$+7$\sqrt{b}$)=0,推出a、b的关系即可解决问题.
解答 解:∵$\sqrt{a}$($\sqrt{a}$-2$\sqrt{b}$)=5$\sqrt{b}$($\sqrt{a}$+6$\sqrt{b}$),
∴a-2$\sqrt{ab}$=5$\sqrt{ab}$+30b,
∴($\sqrt{a}$-10$\sqrt{b}$)($\sqrt{a}$+7$\sqrt{b}$)=0,
∵a>0,b>0,$\sqrt{a}$+7$\sqrt{b}$>0
∴$\sqrt{a}$=10$\sqrt{b}$,a=100b,
∴原式=$\frac{400b+10b+4b}{200b+10b-3b}$=2.
点评 本题考查二次根式的化简求值,解题的关键是灵活应用因式分解求出a、b的关系,然后利用整体代入的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
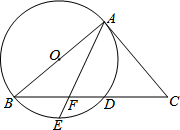 如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
 如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角].
如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角].