题目内容
 如图,△ABC内有三个半径为
如图,△ABC内有三个半径为| 3 |
A、4+3
| ||
B、3+3
| ||
C、4
| ||
D、6+
|
考点:相切两圆的性质
专题:
分析:从各圆心向边作垂线,由题意知△ABC是等边三角形,BD是∠EBF的平分线,可求得BE=BF=DEcot30°=3,AW=AS=CG=CH=3;再根据四边形WFDR,SGTR,THED是矩形,WF=SG=EH=DT=2
,从而求得△ABC的边长,进而求出△ABC的AB边上高的长度.
| 3 |
解答: 解:如图.连接AR、RS、RW、DF、DE,过点C作CO⊥AB于点O,
解:如图.连接AR、RS、RW、DF、DE,过点C作CO⊥AB于点O,
由题意知,△ABC是等边三角形,∠EDB=60°,BD是∠EBF的平分线,
∴∠DBE=30°,BE=BF=DEcot30°=3,
同理,AW=AS=CG=CH=3,四边形WFDR,SGTR,THED是矩形,WF=SG=EH=DT=2
,
∴△ABC的边长为:AB=BC=AC=6+2
,
∴BO=3+
,
则CO=
=3
+3.
故选B.
 解:如图.连接AR、RS、RW、DF、DE,过点C作CO⊥AB于点O,
解:如图.连接AR、RS、RW、DF、DE,过点C作CO⊥AB于点O,由题意知,△ABC是等边三角形,∠EDB=60°,BD是∠EBF的平分线,
∴∠DBE=30°,BE=BF=DEcot30°=3,
同理,AW=AS=CG=CH=3,四边形WFDR,SGTR,THED是矩形,WF=SG=EH=DT=2
| 3 |
∴△ABC的边长为:AB=BC=AC=6+2
| 3 |
∴BO=3+
| 3 |
则CO=
| BO |
| tan30° |
| 3 |
故选B.
点评:本题考查了切线长定理、等边三角形的判定和性质等知识点,得出三角形的边长是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在-3,-
,0,3四个数中,最小的数是( )
| 1 |
| 2 |
| A、-3 | ||
B、-
| ||
| C、0 | ||
| D、3 |
在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕直角边所在直线旋转一周,得到的几何体侧面积是( )
| A、15π | B、12π |
| C、20π | D、15π或20π |
不等式组的解集
在如图中表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图,AOB是直角扇形,以OA、OB为直径在扇形中作圆,n与m分别表示两个阴影部分的面积,那么n、m的大小关系是( )
如图,AOB是直角扇形,以OA、OB为直径在扇形中作圆,n与m分别表示两个阴影部分的面积,那么n、m的大小关系是( )| A、m=n | B、m>n |
| C、m<n | D、无法确定 |
已知|a-6|+
+(c-10)2=0,则这个三角形的形状是( )
| b-8 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 (1)解方程:(1-3y)2+2(3y-1)=0
(1)解方程:(1-3y)2+2(3y-1)=0 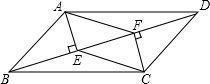 如图:在四边形ABCD中,AB=CD,BF=DE,且AE⊥BD,CF⊥BD,垂足分别为E、F.
如图:在四边形ABCD中,AB=CD,BF=DE,且AE⊥BD,CF⊥BD,垂足分别为E、F.