题目内容
在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕直角边所在直线旋转一周,得到的几何体侧面积是( )
| A、15π | B、12π |
| C、20π | D、15π或20π |
考点:圆锥的计算,点、线、面、体
专题:计算题
分析:先根据勾股定理计算出AB=5,然后分类讨论:当将△ABC绕直角边AC所在直线旋转一周,得到的几何体为圆锥,圆锥的底面圆的半径为4;当将△ABC绕直角边BC所在直线旋转一周,得到的几何体为圆锥,圆锥的底面圆的半径为3,再分别根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
解答:解:∵∠C=90°,AC=3,BC=4,
∴AB=
=5,
当将△ABC绕直角边AC所在直线旋转一周,得到的几何体侧面积=
•2π•4•5=20π;
当将△ABC绕直角边BC所在直线旋转一周,得到的几何体侧面积=
•2π•3•5=15π.
故选D.
∴AB=
| AC2+BC2 |
当将△ABC绕直角边AC所在直线旋转一周,得到的几何体侧面积=
| 1 |
| 2 |
当将△ABC绕直角边BC所在直线旋转一周,得到的几何体侧面积=
| 1 |
| 2 |
故选D.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
 平行四边形ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
平行四边形ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A、3cm | B、6cm |
| C、9cm | D、12cm |
若am=2,an=3,则a2m-n的值是( )
| A、1 | ||
| B、12 | ||
C、
| ||
D、
|
若
是方程组
的解,则a、c的关系是( )
|
|
| A、4c-9a=1 |
| B、9a+4c=1 |
| C、3a+2c=1 |
| D、4c-9a+1=0 |
下列语句中,不是命题的是( )
| A、两点确定一条直线 |
| B、垂线段最短 |
| C、同位角相等 |
| D、做角A的平分线 |
为了了解某市5万名初中毕业生的中考数学成绩,从中抽取1000名学生的数学成绩进行统计分析,在这个问题中下列说法正确的是( )
| A、总体是某市5万名初中毕业生 |
| B、个体是每个初中毕业生的数学成绩 |
| C、样本是从中抽取1000名学生 |
| D、样本容量是1000名 |
 如图,△ABC内有三个半径为
如图,△ABC内有三个半径为| 3 |
A、4+3
| ||
B、3+3
| ||
C、4
| ||
D、6+
|
 已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图,点C也在小方格的顶点上,且以A、B、C为顶点的三角形的面积为1个平方单位,则点C的个数为
已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图,点C也在小方格的顶点上,且以A、B、C为顶点的三角形的面积为1个平方单位,则点C的个数为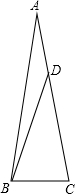 如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数.
如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数.