题目内容
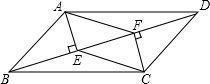 如图:在四边形ABCD中,AB=CD,BF=DE,且AE⊥BD,CF⊥BD,垂足分别为E、F.
如图:在四边形ABCD中,AB=CD,BF=DE,且AE⊥BD,CF⊥BD,垂足分别为E、F.(1)四边形ABCD是平行四边形吗?请说明理由.
(2)四边形ABCF是平行四边形吗?请说明理由.
考点:平行四边形的判定
专题:
分析:(1)首先证明Rt△ABE≌Rt△CDF可得∠ABE=∠CDF,进而得到AB∥CD,再由条件AB=CD可得四边形ABCD是平行四边形;
(2)假设四边形ABCF是平行四边形则AB∥CF,但是∠ABE≠∠BFC,因此AB与CF不平行,因此四边形ABCF是平行四边形.
(2)假设四边形ABCF是平行四边形则AB∥CF,但是∠ABE≠∠BFC,因此AB与CF不平行,因此四边形ABCF是平行四边形.
解答: 证明:(1)四边形ABCD是平行四边形;
证明:(1)四边形ABCD是平行四边形;
∵AE⊥BD,CF⊥BD,
∴∠1=∠2=90°,
∵BF=DE,
∴BF-EF=DE-EF,
即:BE=DF,
在Rt△ABE和Rt△CDF中,
,
∴Rt△ABE≌Rt△CDF(HL),
∴∠ABE=∠CDF,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
(2)四边形ABCF不是平行四边形;
∵∠EFC>∠BDC,∠ABE=∠CDF
∴∠ABE≠∠BFC,
∴AB与CF不平行,
∴四边形ABCF不是平行四边形.
 证明:(1)四边形ABCD是平行四边形;
证明:(1)四边形ABCD是平行四边形;∵AE⊥BD,CF⊥BD,
∴∠1=∠2=90°,
∵BF=DE,
∴BF-EF=DE-EF,
即:BE=DF,
在Rt△ABE和Rt△CDF中,
|
∴Rt△ABE≌Rt△CDF(HL),
∴∠ABE=∠CDF,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
(2)四边形ABCF不是平行四边形;
∵∠EFC>∠BDC,∠ABE=∠CDF
∴∠ABE≠∠BFC,
∴AB与CF不平行,
∴四边形ABCF不是平行四边形.
点评:此题主要考查了平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
若am=2,an=3,则a2m-n的值是( )
| A、1 | ||
| B、12 | ||
C、
| ||
D、
|
 如图,△ABC内有三个半径为
如图,△ABC内有三个半径为| 3 |
A、4+3
| ||
B、3+3
| ||
C、4
| ||
D、6+
|
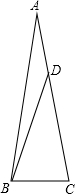 如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数.
如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数. 一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?
一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?