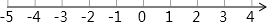题目内容
9. 如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
分析 该图形被平分成四部分,因而每部分被分成的圆心角是90°,并且圆具有旋转不变性,因而旋转90度的整数倍,就可以与自身重合.
解答 解:该图形被平分成四部分,因而每部分被分成的圆心角是90°,旋转90°的整数倍,就可以与自身重合,
因而A、B、D都不正确,不能与其自身重合;能与自身重合的是C.
故选:C.
点评 本题考查旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.

练习册系列答案
相关题目
20.若$\sqrt{a-5}$在实数范围内有意义,则a的取值范围是( )
| A. | a>0 | B. | a>5 | C. | a≥5 | D. | a≤5 |
1.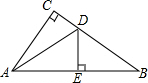 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )
 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,ED⊥AB,且∠CAD:∠BAD=5:2,则∠BAC=( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
5.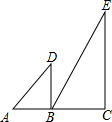 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )| A. | 90° | B. | 45° | C. | 45°或90° | D. | 45°或90°或135° |
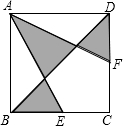 已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几?
已知正方形ABCD,E为BC的中点,DF=$\frac{1}{2}$CF,求阴影部分占正方形面积的几分之几?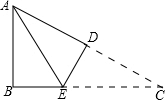 如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.
如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.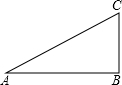 利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.
利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.