题目内容
18.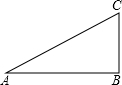 利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.
利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.(1)在数轴上作出表示-$\sqrt{2}$的点(尺规作图,保留痕迹).
(2)在数轴上作出表示$\sqrt{3}$的点(尺规作图,保留痕迹).
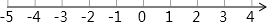
分析 利用勾股定理直接计算即可求出AC的长;
(1)作边长为1的正方形ABOC,连接OA,以O为圆心,以OA为半径画弧交数轴的负半轴于D,即可得到答案.
(2)$\sqrt{3}$可以看作两直角边长分别为1,$\sqrt{2}$的直角三角形的斜边长;而$\sqrt{2}$又可以看作两直角边长分别为1,1的直角三角形的斜边长.
解答 解:∵在Rt△ABC中,AB=2,BC=1,
∴AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$;
(1)如图所示:-$\sqrt{2}$所在的点的位置是D.
(2)如图所示:
①作一个等腰直角三角形,使其两直角边都是1,则斜边为$\sqrt{2}$;
②作一个直角三角形,使其两直角边分别为1,$\sqrt{2}$,则斜边为$\sqrt{3}$;
③在数轴上,以原点O为圆心,$\sqrt{3}$为半径画弧,与数轴正半轴交于点A.
则点A就是所求的点.
点评 本题主要考查对勾股定理,实数与数轴等知识点的理解和掌握,能正确画图是解此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
9. 如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
 如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )
如图,该图形绕点O按下列角度旋转后,能与原图形重合的是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
6.正比例函数y=-3x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
3.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
50名学生平均每天课外阅读时间统计表
| 类别 | A | B | C | D |
| 时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
| 人数 | 5a | 5b | 5c | 5d |
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
13.某工艺品商店购进一款进价为10元/件的工艺品进行试销,经过一段时间的销售得到如下数据:
(1)根据表格中的对应关系,猜想y与x的函数关系,并求出该函数关系式;
(1)当销售单价定为多少时,商店试销该工艺品每天获得的利润最大?(利润=销售总价-成本总价)
(2)若物价部门规定,这种工艺品的销售单价不能超过38元,那么工艺品商店应该将工艺品的销售单价定为多少时,使每天销售该工艺品获得的利润最大?最大利润是多少?
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 50 | 40 | 30 | 20 | 10 | … |
(1)当销售单价定为多少时,商店试销该工艺品每天获得的利润最大?(利润=销售总价-成本总价)
(2)若物价部门规定,这种工艺品的销售单价不能超过38元,那么工艺品商店应该将工艺品的销售单价定为多少时,使每天销售该工艺品获得的利润最大?最大利润是多少?
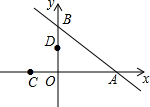 如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记得点C,折痕与y轴交于点D,则点D的坐标为(0,$\frac{4}{3}$).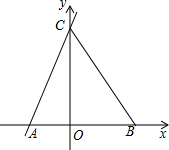 如图,已知点(-2,0),B(3,0),C(0,6),连接BC.
如图,已知点(-2,0),B(3,0),C(0,6),连接BC.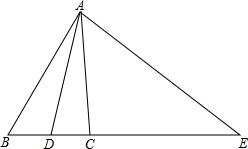 如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.
如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.