题目内容
1．
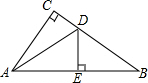如图，在△ABC中，∠C=90°，点E是斜边AB的中点，ED⊥AB，且∠CAD：∠BAD=5：2，则∠BAC=（ ）| A． | 60° | B． | 70° | C． | 80° | D． | 90° |
分析 根据DE是AB的垂直平分线可得，AD=BD，即可求出∠BAD=∠ABD，再根据∠CAD：∠BAD=5：2及直角三角形两锐角的关系解答即可．
解答 解：∵△ABC中，∠ACB=90°，DE是AB的垂直平分线，
∴AD=BD，即∠BAD=∠ABD，
∵∠CAD：∠BAD=5：2，
设∠BAD=2x，则∠CAD=5x，
∵∠BAD+∠CAD+∠ABD=90°，即2x+5x+2x=90°，
解得：x=10°，
∴∠∠BAC=70°．
故选B．
点评 本题主要考查了线段垂直平分线的性质，熟练掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解答此题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
12．5月12日，抚州市某中学进行了全校师生防灾减灾大演练，警报拉响后同学们匀速跑步到操场，在操场指定位置清点人数后，再沿原路匀速步行回教室，同学们离开教学楼的距离y与时间x的关系的大致图象是（ ）
| A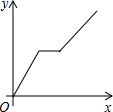． |  | B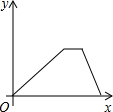． |  | C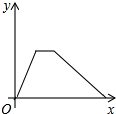． |  | D． |  |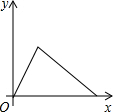
9．
如图，该图形绕点O按下列角度旋转后，能与原图形重合的是（ ）
如图，该图形绕点O按下列角度旋转后，能与原图形重合的是（ ）| A． | 45° | B． | 60° | C． | 90° | D． | 120° |
6．正比例函数y=-3x的大致图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
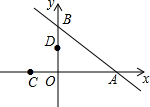如图，在平面直角坐标系xOy中，直线y=-$\frac{3}{4}$x+3与x轴交于点A，与y轴交于点B，将△AOB沿过点A的直线折叠，使点B落在x轴负半轴上，记得点C，折痕与y轴交于点D，则点D的坐标为（0，$\frac{4}{3}$）．
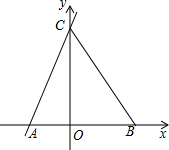如图，已知点（-2，0），B（3，0），C（0，6），连接BC．
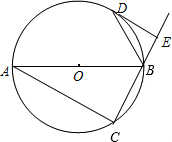已知：如图，△ABC是⊙O的内角三角形，△ABC的外角平分线BD交⊙O于D，DE与⊙O相切，交CB的延长线于E．