题目内容
20．若x=$\frac{1}{\sqrt{2}-1}$，y=$\frac{1}{1+\sqrt{2}}$．求（1）x+y和xy的值；
（2）求x2-xy+y2的值．
分析 首先对x和y的值进行分母有理化，（1）把化简后的x和y的值代入计算即可；
（2）把所求的式子化成（x+y）2-3xy的形式，然后根据（1）的结果计算即可．
解答 解：x=$\frac{1}{\sqrt{2}-1}$=$\frac{\sqrt{2}+1}{（\sqrt{2}-1）（\sqrt{2}+1）}$=$\sqrt{2}$+1，y=$\frac{1}{1+\sqrt{2}}$=$\frac{\sqrt{2}-1}{（1+\sqrt{2}）（\sqrt{2}-1）}$=$\sqrt{2}$-1．
（1）x+y=（$\sqrt{2}$+1）+（$\sqrt{2}$-1）=2$\sqrt{2}$，
xy=（$\sqrt{2}$+1）（$\sqrt{2}$-1）=2-1=1；
（2）原式=（x+y）2-3xy=（2$\sqrt{2}$）2-3×1=8-3=5．
点评 本题考查了二次根式的化简求值，正确进行分母有理化是关键．
练习册系列答案
相关题目
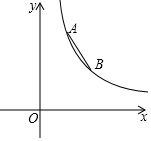如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象上有A、B两点，A点的横坐标为2，B点的横坐标为4，且AB=$\sqrt{13}$．则k的值为（ ）
如图，在一个半径为18cm的圆面上，从中心挖去一个小圆面，当挖去小圆的半径由小变大时，剩下的一个圆环面积也随之发生变化．