题目内容
19.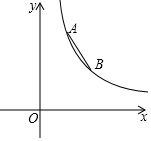 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
分析 由点A、B的横坐标利用反比例函数图象上点的坐标特征即可找出点A、B的坐标,再利用两点间的距离公式结合AB=$\sqrt{13}$即可得出关于k的无理方程,解之即可求出k值,取其正值即可.
解答 解:∵反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,
∴A(2,$\frac{k}{2}$),B(4,$\frac{k}{4}$),
∴AB=$\sqrt{(4-2)^{2}+(\frac{k}{4}-\frac{k}{2})^{2}}$=$\sqrt{13}$,
解得:k=±12,$\sqrt{(4-2)^{2}+(\frac{k}{4}-\frac{k}{2})^{2}}$=$\sqrt{13}$的解.
经检验,k=±12是无理方程
∵反比例函数在第一象限有图象,
∴k=12.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征、无理方程以及两点间的距离公式,根据两点间的距离公式结合AB=$\sqrt{13}$列出关于k的无理方程是解题的关键.

练习册系列答案
相关题目
10.有x辆客车,若每辆客车乘50人,则还有10人不能上车,若每辆车乘52人,则车上只剩2个空位,下列方程中正确的是( )
| A. | 50x-10=52x-2 | B. | 50x+10=52x-2 | C. | 50x+10=52x+2 | D. | 50x-10=52x+2 |
4.下列图形中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点Bn的坐标是(2n-1,2n-1)(n为正整数).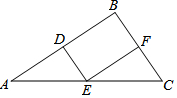 如图,四边形BDEF是直角三角形ABC的内接正方形,如果AB=6,BC=4,求此内接正方形的边长DE.
如图,四边形BDEF是直角三角形ABC的内接正方形,如果AB=6,BC=4,求此内接正方形的边长DE.