题目内容
11. 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为4;
(2)①求点M(3,0)到直线y=2x+1的距离;
②如果点N(0,a)到直线y=2x+1的距离为3,那么a的值是1±3$\sqrt{5}$;
(3)如果点G(0,b)到抛物线y=x2的距离为3,请直接写出b的值.
分析 (1)根据勾股定理可得点O(0,0)到⊙P的距离;
(2)①过点M作MH⊥l,垂足为点H,通过证明△EOF∽△MHE,由相似三角形的性质可得$MH=\frac{{7\sqrt{5}}}{5}$,从而得到点M到直线y=2x+1的距离;
②分两种情况:N在F点的上边;N在F点的下边;进行讨论先得到EN的长,进一步即可得到a的值;
(3)分两种情况:①点G在原点下面;②点G在原点上面;进行讨论即可得到b的值.
解答 解:(1)OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
点O(0,0)到⊙P的距离为5-1=4;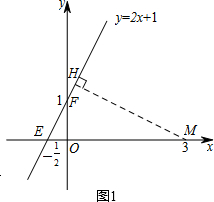 (2)①直线y=2x+1记为l,如图1,过点M作MH⊥l,垂足为点H,
(2)①直线y=2x+1记为l,如图1,过点M作MH⊥l,垂足为点H,
设l与x,y轴的交点分别为E,F,则$E(-\frac{1}{2},0),F(0,1)$.
∴$EF=\frac{{\sqrt{5}}}{2}$.
∵△EOF∽△EHM,
∴$\frac{MH}{OF}=\frac{ME}{EF}$,即$\frac{MH}{1}=\frac{{\frac{7}{2}}}{{\frac{{\sqrt{5}}}{2}}}$.
∴$MH=\frac{{7\sqrt{5}}}{5}$.
∴点M到直线y=2x+1的距离为$\frac{{7\sqrt{5}}}{5}$.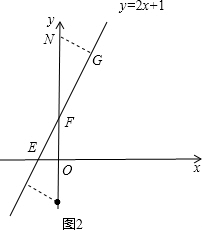 ②N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
②N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
∵△EOF∽△NGF,
∴$\frac{NG}{EO}$=$\frac{NF}{EF}$,即$\frac{3}{\frac{1}{2}}$=$\frac{a-1}{\frac{\sqrt{5}}{2}}$,
∴a=1+3$\sqrt{5}$;
N在F点的下边,
同理可得a=1-3$\sqrt{5}$;
故$a=1±3\sqrt{5}$.
(3)①点G在原点下面,b=-3;
②点G在原点上面,$\sqrt{{x}^{2}+({{x}^{2}-b)}^{2}}$=3,
x4+(1-2b)x2+b2-9=0,
△=(1-2b)2-4(b2-9)=-4b+37=0,
解得$b=\frac{37}{4}$.
故b的值是-3或$\frac{37}{4}$.
故答案为:4;1±3$\sqrt{5}$.
点评 考查了二次函数综合题,涉及的知识点有:勾股定理,相似三角形的判定和性质,根与判别式的关系,两点间的距离公式,方程思想,分类思想,综合性较强,有一定的难度.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | 2a+3a=6a | B. | a2+a3=a5 | C. | a8÷a2=a6 | D. | (a3)4=a7 |
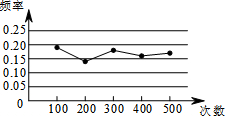 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图的折线图,那么符合这一结果的实验最有可能的是( )
某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图的折线图,那么符合这一结果的实验最有可能的是( )| A. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| B. | 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 | |
| C. | 掷一枚质地均匀的硬币,落地时结果是“正面向上” | |
| D. | 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6 |
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 2 | D. | -3 |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
 把一副常用的三角板如图所示拼在一起,点B在AE上,那么图中∠ABC=75°.
把一副常用的三角板如图所示拼在一起,点B在AE上,那么图中∠ABC=75°.