题目内容
16.(1)计算:$\sqrt{8}$+(-$\frac{1}{2}$)-2-4sin45°+(π-2015)0(2)解不等式组:$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x+1}{2}-1≥x}\end{array}\right.$.
分析 (1)分别根据数的开方法则、负整数指数幂的运算法则及特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=2$\sqrt{2}$+4-4×$\frac{\sqrt{2}}{2}$+1
=2$\sqrt{2}$+4-2$\sqrt{2}$+1
=5;
(2)$\left\{\begin{array}{l}2x-1>5①\\ \frac{3x+1}{2}-1≥x②\end{array}\right.$,由①得,x>3,由②得,x≥1,
故不等式组得解集为:x>3.
点评 本题考查的是实数的运算,熟知数的开方法则、负整数指数幂的运算法则及特殊角的三角函数值是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4. 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )| A. | $\left\{\begin{array}{l}x≥-2\\ x>3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<-2\\ x≤3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ |
8.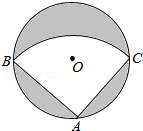 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )| A. | $\frac{{\sqrt{2}}}{2}$米 | B. | $\frac{{\sqrt{2}}}{4}$米 | C. | $\frac{1}{2}$米 | D. | $\frac{1}{4}$米 |
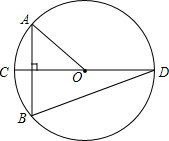 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°. 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.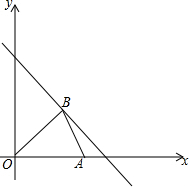 如图,点B是直线y=-x+8在第一象限的一动点,A(6,0),设△AOB的面积为S.
如图,点B是直线y=-x+8在第一象限的一动点,A(6,0),设△AOB的面积为S.