题目内容
19.当x、y、z为非负数,且$\left\{\begin{array}{l}{3x+3y+z=4}\\{x-3y-2z=-3}\end{array}\right.$,求t=3x-2y+z的最大值和最小值.分析 解方程组得到y和z的关于x的表达式,再根据y,z为非负实数,列出关于x的不等式组,求出x的取值范围,再将t转化为关于x的表达式,将x的最大值和最小值代入解析式即可得到t的最大值和最小值.
解答 解:解$\left\{\begin{array}{l}{3x+3y+z=4①}\\{x-3y-2z=-3②}\end{array}\right.$
①+②得,4x-z=1,
则z=4x-1,
将z=4x-1代入①可解得,7x+3y=5,
则y=$\frac{5-7x}{3}$.
因为y,z均为非负数,
所以$\left\{\begin{array}{l}{4x-1≥0}\\{\frac{5-7x}{3}≥0}\end{array}\right.$,
解得$\frac{1}{4}$≤x≤$\frac{5}{7}$.
于是,
t=3x-2y+z=3x-2($\frac{5-7x}{3}$)+(4x-1)
=$\frac{35}{3}$x-$\frac{13}{3}$.
当x值增大时,t的值增大;当x值减小时,t的值减小.
故当x=$\frac{5}{7}$时,t有最大值4;当x=$\frac{1}{4}$时,t有最小值-$\frac{17}{12}$.
点评 此题考查了一次函数最值的求法,将y、z的转化为关于x的表达式及求出x的表达式是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
10.如果(x+1)(2x+m)的乘积中不含x的一次项,则m的值为( )
| A. | 2 | B. | -2 | C. | 0.5 | D. | -0.5 |
4. 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
 如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )
如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是( )| A. | $\left\{\begin{array}{l}x≥-2\\ x>3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<-2\\ x≤3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ |
8.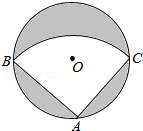 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )| A. | $\frac{{\sqrt{2}}}{2}$米 | B. | $\frac{{\sqrt{2}}}{4}$米 | C. | $\frac{1}{2}$米 | D. | $\frac{1}{4}$米 |
9.金鸡湖景区建设共投资约8 950 000 000元,这个数用科学记数法可表示为( )
| A. | 895×107 | B. | 89.5×108 | C. | 8.95×109 | D. | 0.895×1010 |
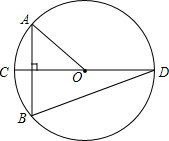 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为20°.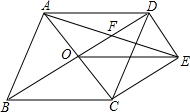 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接 CE、OE,连接AE交OD于点F.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接 CE、OE,连接AE交OD于点F.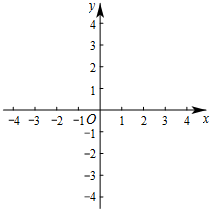 设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.