题目内容
3.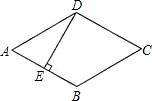 如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.
如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.
分析 利用勾股定理求出DE,根据菱形ABCD的面积=AB•DE计算即可.
解答 解:∵四边形ABCD是菱形,
∴AD=AB=4,
∵AE=EB=2,
∵DE⊥AB,
∴∠AED=90°
在Rt△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=2$\sqrt{3}$,
∴菱形ABCD的面积=AB•DE=4•2$\sqrt{3}$=8$\sqrt{3}$,
故答案为8$\sqrt{3}$.
点评 本题考查菱形的性质,勾股定理,线段的垂直平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
15.下列事件中,必然事件是( )
| A. | 6月14日晚上能看到月亮 | |
| B. | 早晨的太阳从东方升起 | |
| C. | 打开初三数学书本,正好翻到第21页 | |
| D. | 任意掷一枚均匀的硬币,正面朝上 |
12.比-2小1的数是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
13.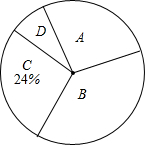 某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
(1)表中的a=0.3,b=6;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
 某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为D的人数约为多少?
 如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.
如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.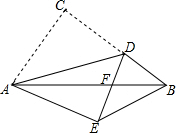 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.