题目内容
12.满足方程|2|2x-4|-3|=2x-1的所有解的和为多少?分析 因为题目中带有绝对值符号,所以必须分两种情况进行讨论,去掉绝对值符号,得到两个一元一次方程,求出方程的根,即可得到结果.
解答 解:①当2x-4≥0时,
方程化为|4x-11|=2x-1,
即4x-11=2x-1或4x-11=1-2x,
解得:x=5,或x=2,
②当2x-4<0时,
方程化为|5-4x|=2x-1,
即5-4x=2x-1,或5-4x=1-2x,
解得:x=1,或x=2(舍去),
故方程|2|2x-4|-3|=2x-1的所有解的和为:5+2+1=8.
点评 本题考查的是含绝对值符号的一元一次方程,由于带有绝对值符号,必须对题目进行讨论,对重复的根要舍去.

练习册系列答案
相关题目
2.在Rt△ABC中,∠C=90°,∠A=60°,AC=6,则BC的长为( )
| A. | 6$\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 12 |
20.对于下列各数:-$\frac{4}{5}$,$\frac{2}{3}$,-6,0,-3.14,-0.25,其中负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.以下列各组线段为边,能组成三角形的是( )
| A. | 4cm,6cm,8cm | B. | 2cm,3cm,5cm | C. | 5cm,6cm,12cm | D. | 1cm,2cm,4cm |

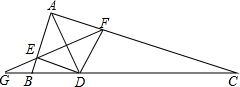 如图,在△ABC中,AC=3AB,AD平分∠BAC,交BC边于点D,DE∥CA,交AB边于点E,DF∥BA,交AC边于点F,FE的延长线与CB的延长线交于点G.
如图,在△ABC中,AC=3AB,AD平分∠BAC,交BC边于点D,DE∥CA,交AB边于点E,DF∥BA,交AC边于点F,FE的延长线与CB的延长线交于点G.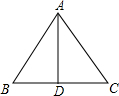 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为55°.
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为55°.