题目内容
15.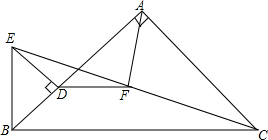 如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,垂足分别为点A、点D,连接EC,F为线段EC的中点,连接DF、AF,则下列说法:①DF⊥AF;②DF=AF;③DF=BE,其中正确的有( )
如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,垂足分别为点A、点D,连接EC,F为线段EC的中点,连接DF、AF,则下列说法:①DF⊥AF;②DF=AF;③DF=BE,其中正确的有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①②正确,连接BF,延长DF交AC于点G,利用等腰三角形的性质得到∠DEF=∠DBF,可证得DG∥BC,得出△ADG为等腰在角形,再证明△DEF≌△GFC得DF=FG,根据三线合一即可得出结论.
解答 证明:连接BF,延长DF交AC于点G,
∵∠EBD=∠ABC=45°,
∴∠EBC=90°,
在RT△EBC中,F为斜边中点,
∴BF=EF,
∴∠FBC=∠FCB,
∴∠DFE=∠DFB,
∵∠EFB=∠FBC+∠FCB,
∴∠DFE+∠DFB=∠FBC+∠FCB,
∴2∠DFB=2∠FBC,
则∠DFB=∠FBC,
∴DG∥BC,
∵△BAC为等腰直角三角形,且DG∥BC,AB=AC,
∴AD=AG,BD=CG,
∵BD=DE,
∴DE=CG,
∵∠BDE=∠CAB=90°,
∴DE∥AC,
∴∠DEF=∠GCF,
在△DEF和△GCF中,
$\left\{\begin{array}{l}{EF=CF}\\{∠DEF=∠GCF}\\{DE=CG}\end{array}\right.$,
∴△DEF≌△GCF(SAS),
∴DF=FG,
∵△DAG为等腰直角三角形,
∴AF⊥DG,AF=DF.
∵BE=$\sqrt{2}$BD,DF=$\frac{\sqrt{2}}{2}$AD,
如图BE=DF那么AD=2BD,显然与条件不符合.
故①②正确,
故选A.
点评 本题主要考查三角形全等的判定和性质、等腰直角三角形的性质,解题的关键是添加辅助线构造全等三角形,证得△ADG为等腰三角形.

练习册系列答案
相关题目
10.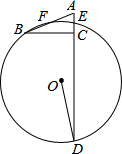 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 13 | B. | $2\sqrt{26}$ | C. | $3\sqrt{26}$ | D. | $\frac{27}{2}$ |
 一个直棱柱的三视图如图所示(单位:mm),请描述这个直棱柱的形状,并画出它的表面展开图,求出它的表面积(结果保留3个有效数字).
一个直棱柱的三视图如图所示(单位:mm),请描述这个直棱柱的形状,并画出它的表面展开图,求出它的表面积(结果保留3个有效数字). 如图,∠D=30°,∠O=50°,∠C=35°,则∠AEC等于65°.
如图,∠D=30°,∠O=50°,∠C=35°,则∠AEC等于65°.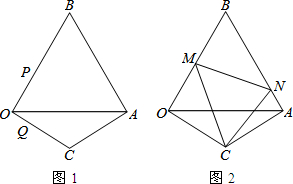
 如图,∠1和∠3是直线a、b被直线c所截得到的同旁内角;
如图,∠1和∠3是直线a、b被直线c所截得到的同旁内角;