题目内容
4．知|x+3|与|2y-3|互为相反数，求x-y的值．分析 根据互为相反数的两个数的性质可知：互为相反数的两个数的和0，再结合绝对值的意义分析：几个非负数的和为0，它们同时为0．
解答 解：∵|x+3|与|2y-3|互为相反数，
∴|x+3|与|2y-3|=0，
∴x+3=0，2y-3=0，
∴x=-3，y=$\frac{3}{2}$．
∴x-y=-$\frac{9}{2}$．
点评 题考查了相反数的概念、绝对值的性质和非负数的性质，掌握相反数之和为0和有限个非负数的和为零，那么每一个加数也必为零是解题的关键．
练习册系列答案
相关题目
如图，已知∠α，∠β．求作∠ABC．
15．
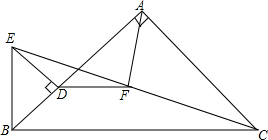如图，△ABC与△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，垂足分别为点A、点D，连接EC，F为线段EC的中点，连接DF、AF，则下列说法：①DF⊥AF；②DF=AF；③DF=BE，其中正确的有（ ）
如图，△ABC与△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，垂足分别为点A、点D，连接EC，F为线段EC的中点，连接DF、AF，则下列说法：①DF⊥AF；②DF=AF；③DF=BE，其中正确的有（ ）| A． | ①② | B． | ①③ | C． | ②③ | D． | ①②③ |
12．
如图，以AC为斜边在异侧作Rt△ABC和Rt△ADC，∠ABC=∠ADC=90°，∠BCD=45°，BD=4，则AC的长度为（ ）
如图，以AC为斜边在异侧作Rt△ABC和Rt△ADC，∠ABC=∠ADC=90°，∠BCD=45°，BD=4，则AC的长度为（ ）| A． | 8 | B． | 4$\sqrt{2}$ | C． | 6 | D． | $\sqrt{2}$ |
如图，直线L1，L2交于一点P，若y1≥y2，则x的取值范围是x≤3．
16．
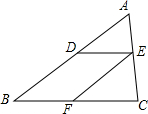如图，在△ABC中，DE∥BC，若AD=1，BD=2，则$\frac{DE}{BC}$的值为（ ）
如图，在△ABC中，DE∥BC，若AD=1，BD=2，则$\frac{DE}{BC}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |