题目内容
4.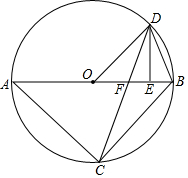 如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若$\frac{S_1}{S_2}$=$\frac{2}{7}$,求sinA的值.
分析 (1)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得出即可;
(2)根据相似三角形的性质得出∠ODE=∠A,根据圆周角定理得出∠A=∠BDC,推出∠ODE=∠BDC即可;
(3)根据△DOE~△ABC求出S△ABC=4S△DOE=4S1,求出S△BOC=2S1,求出2BE=OE,解直角三角形求出即可.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC;
(2)证明:∵△DOE~△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是$\widehat{BC}$所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE~△ABC,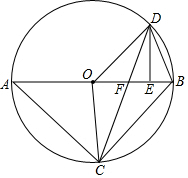
∴$\frac{{{S_{△DOE}}}}{{{S_{△ABC}}}}={({\frac{OD}{AB}})^2}=\frac{1}{4}$,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴${S_{△BOC}}=\frac{1}{2}{S_{△ABC}}$,即S△BOC=2S1,
∵$\frac{S_1}{S_2}=\frac{2}{7},{S_2}={S_{△BOC}}+{S_{△DOE}}+{S_{△DBE}}=2{S_1}+{S_1}+{S_{△DBE}}$,
∴${S_{△DBE}}=\frac{1}{2}{S_1}$,
∴$BE=\frac{1}{2}OE$,
即$OE=\frac{2}{3}OB=\frac{2}{3}OD$,
∴$sinA=sin∠ODE=\frac{OE}{OD}=\frac{2}{3}$.
点评 本题考查了相似三角形的性质和判定,圆周角定理,平行线的性质,三角形的面积等知识点,能综合运用知识点进行推理是解此题的关键.

 阅读快车系列答案
阅读快车系列答案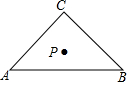 如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
| A. | b>2 | B. | b>-2 | C. | b<2 | D. | b<-2 |
| A. | a和b同号 | B. | a和b异号 | ||
| C. | a和b可能同号也可能异号 | D. | a≠0,b=0 |
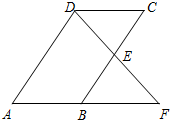 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.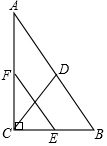 如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是2.
如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是2.