题目内容
9.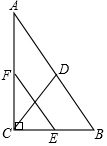 如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是2.
如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是2.
分析 首先利用直角三角形斜边上的中线等于斜边的一半求得AB的长,然后根据三角形的中位线定理求解.
解答 解:∵Rt△ABC中,∠ACB=90°,D是AB的中点,即CD是直角三角形斜边上的中线,
∴AB=2CD=2×2=4,
又∵E、F分别是BC、CA的中点,即EF是△ABC的中位线,
∴EF=$\frac{1}{2}$AB=$\frac{1}{2}$×2=2,
故答案为:2.
点评 本题考查了直角三角形的性质以及三角形的中位线定理,求得AB的长是本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
19.3-π的绝对值是( )
| A. | 3-π | B. | π-3 | C. | 3 | D. | π |
20.已知2x=3y(y≠0),则下面结论成立的是( )
| A. | $\frac{x}{y}$=$\frac{3}{2}$ | B. | $\frac{x}{3}$=$\frac{2}{y}$ | C. | $\frac{x}{y}$=$\frac{2}{3}$ | D. | $\frac{x}{2}$=$\frac{y}{3}$ |
19.已知反比例函数y=$\frac{k}{x}$的图象在第二、第四象限内,函数图象上有两点A(8,y1)、B(5,y2),则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
20. 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )
 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A. | ∠1和∠4是同位角 | B. | ∠1和∠3是同位角 | ||
| C. | ∠1和∠2是同旁内角 | D. | ∠5和∠6是内错角 |
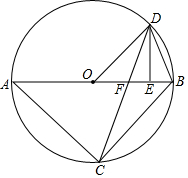 如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.