题目内容
12．若点A（m，n）在一次函数y=3x+b的图象上，且3m-n＞2，则b的取值范围为（ ）| A． | b＞2 | B． | b＞-2 | C． | b＜2 | D． | b＜-2 |
分析 由点A的坐标结合一次函数图象上点的坐标特征，可得出3m+b=n，再由3m-n＞2，即可得出b＜-2，此题得解．
解答 解：∵点A（m，n）在一次函数y=3x+b的图象上，
∴3m+b=n．
∵3m-n＞2，
∴-b＞2，即b＜-2．
故选D．
点评 本题考查了一次函数图象上点的坐标特征，根据一次函数图象上点的坐标特征结合3m-n＞2，找出-b＞2是解题的关键．
练习册系列答案
相关题目
20．已知2x=3y（y≠0），则下面结论成立的是（ ）
| A． | $\frac{x}{y}$=$\frac{3}{2}$ | B． | $\frac{x}{3}$=$\frac{2}{y}$ | C． | $\frac{x}{y}$=$\frac{2}{3}$ | D． | $\frac{x}{2}$=$\frac{y}{3}$ |
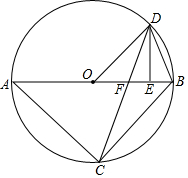如图，已知△ABC内接于⊙O，AB是直径，点D在⊙O上，OD∥BC，过点D作DE⊥AB，垂足为E，连接CD交OE边于点F．