题目内容
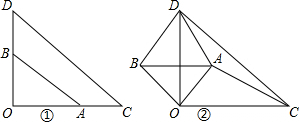
如图1,Rt△OCD中,∠COD=90°,OC=OD,点A、B分别在OC、OD上,且AB∥DC.将△OAB绕点O逆时针旋转,如图2,连接AC、BD,若OA=1,AD=
,AC=2,求∠DAO的度数及点A到OC的高.
| 2 |

考点:旋转的性质
专题:计算题
分析:在如图①中,利用OC=OD,AB∥DC得到△OAB为等腰直角三角形,则OA=OB=1,AB=
OA=
,∠OAB=45°;在如图②中,由于∠AOB=∠COD=90°,OA=OB,OC=OD,根据旋转的定义,可把△AOC绕点O逆时针旋转90°可得到△BOD,则BD=AC=2,则可根据勾股定理的逆定理证明△ABD为直角三角形,∠BAD=90°,于是得到∠DAO=∠DAB+∠OAB=135°;作OH⊥DA于H,如图②,易得△AOH为等腰直角三角形,则AH=OH=
OA=
,再在Rt△ODH中,根据勾股定理计算出OD=
,所以OC=OD=
,然后利用S△BDO+S△DAO=S△ABD+S△OAB可计算出S△BDO=1,则S△OAC=1,最后根据三角形面积公式可求出点A到OC的高.
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 5 |
| 5 |
解答: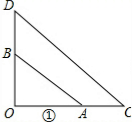 解:如图①,∵Rt△OCD中,∠COD=90°,OC=OD,
解:如图①,∵Rt△OCD中,∠COD=90°,OC=OD,
∴△OCD为等腰直角三角形,
∵AB∥DC,
∴△OAB为等腰直角三角形,
∴OA=OB=1,AB=
OA=
,∠OAB=45°;
∵△OAB绕点O逆时针旋转,如图②,
∴∠AOB=∠COD=90°,
而OA=OB,OC=OD,
∴把△AOC绕点O逆时针旋转90°可得到△BOD,
∴BD=AC=2,
在△ABD中,∵AD=
,AB=
,BD=2,
∴AD2+AB2=BD2,
∴△ABD为直角三角形,∠BAD=90°,
∴∠DAO=∠DAB+∠OAB=135°;
作OH⊥DA于H,如图②,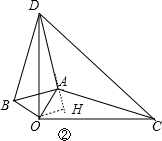
∵∠OAH=180°-∠DAO=45°,
∴△AOH为等腰直角三角形,
∴AH=OH=
OA=
,
在Rt△ODH中,∵OH=
,DH=DA+OH=
,
∴OD=
=
,
∴OC=OD=
,
∵S△BDO+S△DAO=S△ABD+S△OAB,
∴S△BDO+
•
•
=
•
•
+
•1•1,
∴S△BDO=1,
∵△OBD≌△OAC,
∴S△OAC=1,
设点A到OC的高为h,则
•h•
=1,
解得h=
,
∴∠DAO的度数为135°,点A到OC的高为
.
 解:如图①,∵Rt△OCD中,∠COD=90°,OC=OD,
解:如图①,∵Rt△OCD中,∠COD=90°,OC=OD,∴△OCD为等腰直角三角形,
∵AB∥DC,
∴△OAB为等腰直角三角形,
∴OA=OB=1,AB=
| 2 |
| 2 |
∵△OAB绕点O逆时针旋转,如图②,
∴∠AOB=∠COD=90°,
而OA=OB,OC=OD,
∴把△AOC绕点O逆时针旋转90°可得到△BOD,
∴BD=AC=2,
在△ABD中,∵AD=
| 2 |
| 2 |
∴AD2+AB2=BD2,
∴△ABD为直角三角形,∠BAD=90°,
∴∠DAO=∠DAB+∠OAB=135°;
作OH⊥DA于H,如图②,

∵∠OAH=180°-∠DAO=45°,
∴△AOH为等腰直角三角形,
∴AH=OH=
| ||
| 2 |
| ||
| 2 |
在Rt△ODH中,∵OH=
| ||
| 2 |
3
| ||
| 2 |
∴OD=
| OH2+DH2 |
| 5 |
∴OC=OD=
| 5 |
∵S△BDO+S△DAO=S△ABD+S△OAB,
∴S△BDO+
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
∴S△BDO=1,
∵△OBD≌△OAC,
∴S△OAC=1,
设点A到OC的高为h,则
| 1 |
| 2 |
| 5 |
解得h=
2
| ||
| 5 |
∴∠DAO的度数为135°,点A到OC的高为
2
| ||
| 5 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
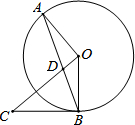 如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.
如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由. 如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S.
如图,直线a表示一条公路,点A、B表示两个乡镇,如果要在公路旁(直线a上)修一个车站S,使得AS=BS,请作出点S. 如图,AB=AC,BD=DC,若∠B=38°,则∠C
如图,AB=AC,BD=DC,若∠B=38°,则∠C 如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,AB=CD.求证:EG=FG.
如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,AB=CD.求证:EG=FG.