题目内容
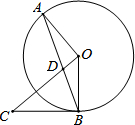 如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.
如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.考点:切线的性质
专题:
分析:由BC是⊙O的切线,得出∠OBC=90°,再由BC=DC,OA=OB,得出∠CBD=∠CDB,∠OAB=∠OBA,再由∠BDC=∠ADO,最后利用等量代换得出∠OAD+∠ADO=90°,进一步得出∠AOC=90°证得OA与OC的位置关系.
解答:解:OA与OC垂直.
理由∵BC是⊙O的切线,
∴∠OBC=90°,
∵BC=DC,OA=OB,
∴∠CBD=∠CDB,∠OAB=∠OBA,
又∵∠BDC=∠ADO,
∴∠OBC=∠OBA+∠CBD=∠OAD+∠ADO=90°,
∴∠AOC=90°,
∴OA⊥OC.
理由∵BC是⊙O的切线,
∴∠OBC=90°,
∵BC=DC,OA=OB,
∴∠CBD=∠CDB,∠OAB=∠OBA,
又∵∠BDC=∠ADO,
∴∠OBC=∠OBA+∠CBD=∠OAD+∠ADO=90°,
∴∠AOC=90°,
∴OA⊥OC.
点评:此题考查切线的性质,等腰三角形的性质以及三角形的内角和定理,利用等量代换是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为
在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为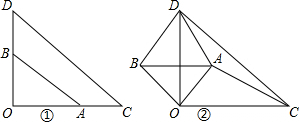
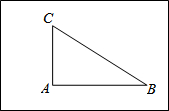 小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上. 已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE.
已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE.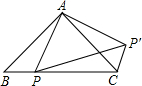 如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=
如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=