题目内容
 如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,AB=CD.求证:EG=FG.
如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,AB=CD.求证:EG=FG.考点:全等三角形的判定与性质
专题:证明题
分析:根据题干给出的条件可以证明△ABF≌△CDE,可得:DE=BF,再根据DE⊥AC,BF⊥AC,∠EGD=∠FGB,可以证明△DEG≌△BFG,可以证明EG=FG.
解答:解:∵AE=CF,AF=AE+EF.CE=CF+FE,
∴AF=CE,
在RT△ABF和RT△CDE中,
,
∴RT△ABF≌RT△CDE(HL),
∴DE=BF;
∵DE⊥AC,BF⊥AC,
∴∠DEG=∠BFG=90°,
在△DEG和△BFG中,
,
∴△DEG≌△BFG(AAS),
∴EG=FG.
∴AF=CE,
在RT△ABF和RT△CDE中,
|
∴RT△ABF≌RT△CDE(HL),
∴DE=BF;
∵DE⊥AC,BF⊥AC,
∴∠DEG=∠BFG=90°,
在△DEG和△BFG中,
|
∴△DEG≌△BFG(AAS),
∴EG=FG.
点评:本题考查了全等三角形的判定,考查了直角三角形全等的判定,考查了全等三角形对应边相等的性质,本题中熟练求证全等三角形是解题的关键.

练习册系列答案
相关题目
如果|2a|=-2a,那么a一定是( )
| A、a<0 | B、a≥0 |
| C、a≤0 | D、a>0 |
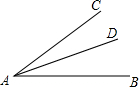 如图,∠BAC=40°,AD平分∠BAC,点P为射线AB上一动点,且△PAD是等腰三角形,则∠APD的度数为
如图,∠BAC=40°,AD平分∠BAC,点P为射线AB上一动点,且△PAD是等腰三角形,则∠APD的度数为 已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE.
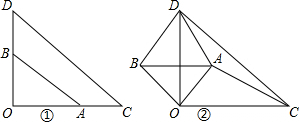
已知,如图,AB⊥BD于B,ED⊥BD于D,且AB=CD,AC=CE.求证:(1)△ABC≌△CDE;(2)AC⊥CE. 如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是
如图,等腰直角三角形ABC经过旋转得到△DBE,∠ACB和∠E都是直角,那么逆时针旋转的角度是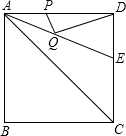 如图,正方形ABCD的边长为8,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是( )
如图,正方形ABCD的边长为8,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是( )