题目内容
 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=| 9 |
| x |
(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,A1A2…An-1An,都在x轴上,
(1)求P1的坐标.
(2)求A2的坐标.
(3)直接写出An的坐标.
考点:反比例函数综合题
专题:综合题
分析:(1)如图,过点P1作P1M⊥x轴,由△OP1A1为等腰直角三角形,利用等腰直角三角形的性质得到P1M=OM=MA1,设P1的坐标是(a,a),a>0,代入反比例解析式求出a的值,即可确定出P1的坐标;
(2)如图,过点P2作P2N⊥x轴,根据OM+A1M求出OA1的长,确定出A1的坐标,再由△P2A1A2为等腰直角三角形,设P2的纵坐标为b,则P2横坐标为6+b,代入反比例解析式求出b的长,即可确定出A2的坐标;
(3)同理确定出A3,A4的坐标,归纳总结得到An的坐标即可.
(2)如图,过点P2作P2N⊥x轴,根据OM+A1M求出OA1的长,确定出A1的坐标,再由△P2A1A2为等腰直角三角形,设P2的纵坐标为b,则P2横坐标为6+b,代入反比例解析式求出b的长,即可确定出A2的坐标;
(3)同理确定出A3,A4的坐标,归纳总结得到An的坐标即可.
解答: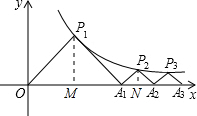 解:(1)如图,过点P1作P1M⊥x轴,
解:(1)如图,过点P1作P1M⊥x轴,
∵△OP1A1是等腰直角三角形,
∴P1M=OM=MA1,
设P1的坐标是(a,a),a>0,
把(a,a)代入解析式y=
(x>0)中,得a=3,
则P1的坐标是(3,3);
(2)如图,过点P2作P2N⊥x轴,
∵OM=MA1=3,
∴OA1=6,即A1的坐标是(6,0),
∵△P2A1A2为等腰直角三角形,
∴P2N=A1N=A2N,
设P2的纵坐标为b,则P2横坐标为6+b,
把(6+b,b)代入函数解析式得:b=
,
解得:b=6
-3,
∴A2的横坐标为6+2b=6+6
-6=6
,
则A2的坐标为(6
,0);
(3)同(2)中的方法得到A3(6
,0),A4(6
,0),
归纳总结得:An的横坐标是6
.
 解:(1)如图,过点P1作P1M⊥x轴,
解:(1)如图,过点P1作P1M⊥x轴,∵△OP1A1是等腰直角三角形,
∴P1M=OM=MA1,
设P1的坐标是(a,a),a>0,
把(a,a)代入解析式y=
| 9 |
| x |
则P1的坐标是(3,3);
(2)如图,过点P2作P2N⊥x轴,
∵OM=MA1=3,
∴OA1=6,即A1的坐标是(6,0),
∵△P2A1A2为等腰直角三角形,
∴P2N=A1N=A2N,
设P2的纵坐标为b,则P2横坐标为6+b,
把(6+b,b)代入函数解析式得:b=
| 9 |
| 6+b |
解得:b=6
| 2 |
∴A2的横坐标为6+2b=6+6
| 2 |
| 2 |
则A2的坐标为(6
| 2 |
(3)同(2)中的方法得到A3(6
| 3 |
| 4 |
归纳总结得:An的横坐标是6
| n |
点评:此题属于反比例函数综合题,涉及的知识有:等腰直角三角形的判定与性质,坐标与图形性质,以及反比例函数的性质,熟练掌握等腰直角三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中错误的命题为( )
| A、圆既是轴对称图形,也是中心对称图形 |
| B、长度相等的弧是等弧 |
| C、三角形的外心是三角形三边垂直平分线的交点 |
| D、半圆是弧 |
二次函数y=-
(x-3)2+5的开口方向、对称轴、顶点坐标分别是( )
| 1 |
| 2 |
| A、向下、直线x=3、(3,5) |
| B、向上、直线x=-3、(-3,5) |
| C、向上、直线x=3、(3,5) |
| D、向下、直线x=-3、(-3,-5) |
某厂一月份的总产量为600吨,三月份的总产量达到980吨.若平均每月增长率是x,则可列方程( )
| A、600(1+x)2=980 |
| B、600(1+2x)=980 |
| C、600(1+x2)=980 |
| D、980(1+x)2=600 |
将方程x2-6x+2=0配方后,原方程变形为( )
| A、(x+3)2=-2 |
| B、(x-3)2=-2 |
| C、(x-3)2=7 |
| D、(x+3)2=7 |
如果|2a|=-2a,那么a一定是( )
| A、a<0 | B、a≥0 |
| C、a≤0 | D、a>0 |
 如图,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,若BD=8cm,CE=9cm,则DE=
如图,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,若BD=8cm,CE=9cm,则DE= 在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为
在菱形ABCD中,点F是AB边上一点,将△ADF沿DF翻折,点A与点G重合,DG的延长线交BC于E,E为BC边的中点,CF=4,则线段EG的长为