题目内容
12.如图,抛物线y=ax2-3ax+c与x轴交于A、B两点,与y轴正半轴交于点C,抛物线的对称轴交x轴于点G,已知B(4,0),tan∠OAC=2.(1)求抛物线的解析式;
(2)将∠CAB绕点A顺时针旋转,边AB旋转后与对称轴相交于点D,边AC旋转后与抛物线相交于点E,与对称轴相交于点F.
①当点F恰好为BC与对称轴的交点时,求点D坐标;
②当AG=DG时,求点E坐标.
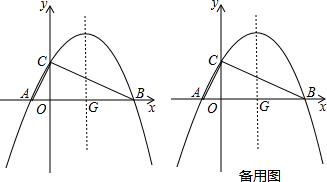
分析 (1)求出对称轴后求出点A坐标,根据tan∠CAO=2求出点C坐标,然后把B、C代入抛物线解析式即可解决问题.
(2)①在RT△ACF中利用勾股定理求出线段AF,CF,再利用△CAF∽△GAD列出比例式即可解决问题.
②求出直线AM,解方程组求交点E的坐标.
解答 (1)解:∵对称轴x=-$\frac{-3a}{2a}$=$\frac{3}{2}$,点B坐标(4,0),
∴点A坐标(1,0),
∵tan∠CAO=2,
∴CO=2AO=2,
∴点C坐标(0,2),
把B、C坐标代入y=ax2-3ax+c得到$\left\{\begin{array}{l}{c=2}\\{16a-12a+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2
(2)①如图1中,设AF=FB=x,
在RT△ACF中,∵AC2+CF2=AF2,
∵AC=$\sqrt{5}$,BC=2$\sqrt{5}$,
∴5+(2$\sqrt{5}$-x)2=x2,
∴x=$\frac{5\sqrt{5}}{4}$,
∴AF=BF=$\frac{5\sqrt{5}}{4}$,CF=$\frac{3\sqrt{5}}{4}$,
∵AC2+BC2=5+20=25,AB2=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴∠ACF=∠AGD,
∵∠CAF=∠GAD,
∴△CAF∽△GAD,
∴$\frac{AC}{AG}=\frac{CF}{GD}$,
∴$\frac{\sqrt{5}}{\frac{5}{2}}=\frac{\frac{3\sqrt{5}}{4}}{DG}$,
∴DG=$\frac{15}{8}$,
∴点D坐标($\frac{3}{2}$,-$\frac{15}{8}$).
②如图2中,∵AG=GD,∠AGD=90°,
∴∠GAD=∠GDA=45°,
∴∠CAM=∠GAD=45°,
∵∠ACM=90°,
∴∠CAM=∠CMA=45°,
∴AC=CM=$\sqrt{5}$,BC=2$\sqrt{5}$,
∴CM=BM,
∴点M坐标为(2,1),
∴直线AM为y=$\frac{1}{3}$x+$\frac{1}{3}$,
由$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{1}{3}}\\{y=-\frac{1}{2}{x}^{2}+\frac{3}{2}x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{13}{9}}\end{array}\right.$,
∴点E坐标($\frac{10}{3}$,$\frac{13}{9}$).
点评 本题考查待定系数法确定二次函数解析式、相似三角形的判定和性质、三角函数的定义、勾股定理等知识,利用相似三角形是解决问题的关键,记住求交点坐标的方法是解方程组,属于中考压轴题.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=2 | D. | 直线x=-2 |
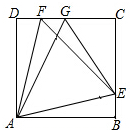 已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG.
已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG. 如图1是一个正方体的展开图,若将这个展开图再折成正方体放在桌面上,如图2所示,则从上面看到的面为( )
如图1是一个正方体的展开图,若将这个展开图再折成正方体放在桌面上,如图2所示,则从上面看到的面为( )