题目内容
1.若把代数式x2+2bx+4化为(x-m)2+k的形式,其中m、k为常数,则k-m=-b2+b+4,k-m的最大值是$\frac{17}{4}$.分析 首先把代数式x2+2bx+4变为x2+2bx+b2-b2+4,再进一步利用完全平方公式,把前三项因式分解化为(x-m)2+k的形式,求出m、k的数值,从而求得k-m的值,根据k-m的顶点式即可求得最大值.
解答 解:x2+2bx+4
=x2+2bx+b2-b2+4
=(x+b)2-b2+4;
∴m=-b,k=-b2+4,
则k-m=-b2+b+4,
∵-b2+b+4=-(b-$\frac{1}{2}$)2+$\frac{17}{4}$.
∴当b=$\frac{1}{2}$时,k-m的最大值是$\frac{17}{4}$.
故答案为:$4-{b^2}+b,\frac{17}{4}$.
点评 此题考查利用完全平方公式配方,注意代数式的恒等变形.

练习册系列答案
相关题目
9.如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
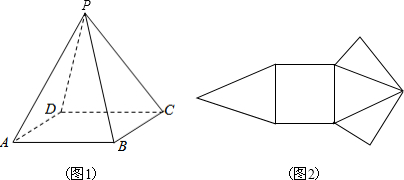

| A. | PA,PB,AD,BC | B. | PD,DC,BC,AB | C. | PA,AD,PC,BC | D. | PA,PB,PC,AD |
13.化简${(-\sqrt{5})^2}$的结果是( )
| A. | 25 | B. | -5 | C. | 5 | D. | ±5 |
10.下列运算结果是负数的是( )
| A. | (-3)×(-2) | B. | (-3)2÷3 | C. | |-3|÷6 | D. | -3-2×(+4) |
 为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.
为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.