题目内容
15.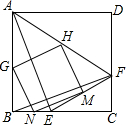 如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.
如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.(1)猜想四边形GHMN的形状?并说明理由.
(2)若AB=4,CF=2,求四边形GHMN的面积.
分析 (1)根据正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,判定△ABE≌△BCF(SAS),可得AE=BF,∠BAE=∠CBF,进而得出AE⊥BF,再根据点G、H、M、N分别是AB,AF,EF,BE的中点,可得四边形GHMN是正方形;
(2)根据勾股定理,可得Rt△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=2$\sqrt{5}$,进而得出GN=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$,据此可得正方形GHMN的面积.
解答  解:(1)四边形GHMN为正方形,理由如下:
解:(1)四边形GHMN为正方形,理由如下:
∵正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,
∴AB=BC,∠ABE=∠BCF=90°,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{BE=CF}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
又∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴AE⊥BF,
∵点G、H、M、N分别是AB,AF,EF,BE的中点,
∴GN=HM=$\frac{1}{2}$AE=$\frac{1}{2}$BF=GH=MN,GH∥BF,GN∥AE,
∴四边形GHMN是菱形,∠HGN=90°,
∴四边形GHMN是正方形;
(2)∵BE=CF=2,AB=4,∠ABE=90°,
∴Rt△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=2$\sqrt{5}$,
∴GN=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$,
∴正方形GHMN的面积=NG2=5.
点评 本题主要考查了中点四边形,正方形的判定,全等三角形的判定与性质以及勾股定理的运用,解题时注意:全等三角形的对应角相等,对应边相等;有一个角是直角的菱形是正方形.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
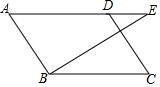 如图,?ABCD中,BE⊥AB于点B,交AD的延长线于点E,若CD=6,tan∠C=$\frac{4}{3}$,则BE=( )
如图,?ABCD中,BE⊥AB于点B,交AD的延长线于点E,若CD=6,tan∠C=$\frac{4}{3}$,则BE=( )| A. | 10 | B. | 8 | C. | 6 | D. | $\frac{9}{2}$ |
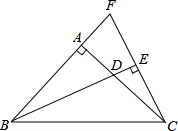 如图,在△ABC中,∠BAC=90°,AB=AC,D为AC边上一点,作EC⊥BD于E,交BA的延长线于F,则有( )
如图,在△ABC中,∠BAC=90°,AB=AC,D为AC边上一点,作EC⊥BD于E,交BA的延长线于F,则有( )| A. | △ABD≌△ACF | B. | △BEF≌△CAF | C. | △BEC≌△BEF | D. | △ABD≌△EBC |
| A. | -2 | B. | 5 | C. | -10 | D. | -5 |
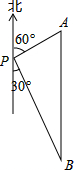 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处于灯塔P之间的距离为30$\sqrt{3}$海里.
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处于灯塔P之间的距离为30$\sqrt{3}$海里.
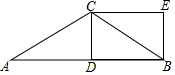 如图,在△ABC中,AC=BC,CD平分∠ACB交AB于D,CE∥AB,且CE=$\frac{1}{2}$AB.
如图,在△ABC中,AC=BC,CD平分∠ACB交AB于D,CE∥AB,且CE=$\frac{1}{2}$AB.