题目内容
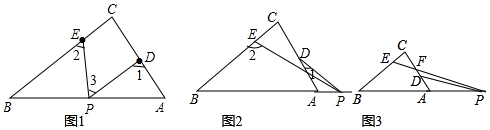
4.如图,在△ABC中,∠ACB=90°,D、E分别是边AC、BC上一点,点P是AB所在直线上一动点,记∠PDA=∠1、∠PEB=∠2、∠DPE=∠3.(1)如图1,若点P在A、B两点之间,连接CP、则∠3与∠1+∠2之间有何数量关系?请说明理由;
(2)若点P在BA的延长线上,且CE<CD.
①当点P在图2所示位置时,∠1、∠2、∠3之间有何数量关系?请说明理由;
②当点P在图3所示位置时,①中结论是否成立?若成立,请说明理由;若不成立,写出此时∠1、∠2、∠3之间的数量关系并说明理由.
分析 (1)如图1中,结论:∠1+∠2=90°+∠3.连接AC,利用三角形的外角的性质证明即可;
(2)①如图2中,结论:∠2=90°+∠1+∠3.利用三角形的外角的性质证明即可;
②如图3中,结论:①中的结论不成立.结论:∠2=90°+∠1-∠3,证明方法类似;
解答 解:(1)如图1中,结论:∠1+∠2=90°+∠3.
理由:连接AC.
∵∠2=∠ECP+∠EPC,∠1=∠DCP+∠DPC,∠3=∠EPC+∠DPC,∠ACB=∠ECP+∠DCP=90°,
∴∠1+∠2=(∠ECP+∠DCP)+(∠EPC+∠DPC)=90°+∠3.
(2)①如图2中,结论:∠2=90°+∠1+∠3.
理由:∵∠2=∠C+∠CFE=90°+∠CFE,
又∵∠CFE=∠1+∠3,
∴∠2=90°+∠1+∠3.
②如图3中,结论:①中的结论不成立.结论:∠2=90°+∠1-∠3.
理由:∵∠2=∠C+∠CFE=90°+∠CFE,
又∵∠1=∠DFP+∠3,∠CFE=∠DFP,
∴∠CFE=∠1-∠3,
∴∠2=90°+∠1-∠3.
点评 此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,∠3转化到一个三角形或四边形中,是一道比较简单的中考常考题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
12.在平面直角坐标系中,点(-6,-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.若反比例函数y=$\frac{k}{x}$(k<0)的图象经过点(-2,y1),(-1,y2),(2,y3),则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
9.下列式子一定是二次根式的是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{{x}^{2}-2}$ |
13.下列说法中,一定正确的为( )
①掷一枚质地均匀的硬币,正面朝上;②甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定;③任何实数的零次幂为1;④对角线相等且互相垂直的四边形是菱形;⑤圆内接四边形的对角互补.
①掷一枚质地均匀的硬币,正面朝上;②甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定;③任何实数的零次幂为1;④对角线相等且互相垂直的四边形是菱形;⑤圆内接四边形的对角互补.
| A. | ①② | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
14.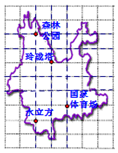 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
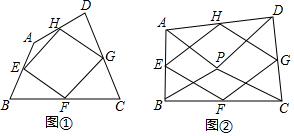
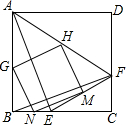 如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.
如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.