题目内容
3.若关于x的分式方程$\frac{2x-a}{x-2}$=$\frac{1}{2}$的解为非负数,则a的取值范围在数轴上表示为( )| A. | 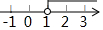 | B. | 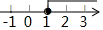 | C. | 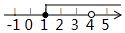 | D. | 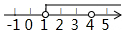 |
分析 首先根据解分式方程的方法,求出分式方程的解是多少;然后根据x≥0,求出a的取值范围即可.
解答 解:去分母,可得:2(2x-a)=x-2,
去括号,可得:4x-2a=x-2
移项,合并同类项,可得:3x=2a-2
解得x=$\frac{2a-2}{3}$,
经检验,x=$\frac{2a-2}{3}$是原方程的解,
∵x=$\frac{2a-2}{3}$≥0,
∴a≥1,
∵x-2≠0,
∴x≠2,
∴$\frac{2a-2}{3}$≠2,
解得a≠4,
∴a≥1且a≠4,
a的取值范围在数轴上表示为: .
.
故选:C.
点评 此题主要考查了分式方程的解,要熟练掌握,注意:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
相关题目
13.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
11.计算(-1)2017+(-$\frac{1}{2}$)-3-(2017)0的结果是( )
| A. | -10 | B. | -8 | C. | 8 | D. | -9 |
18.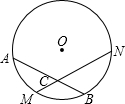 如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
 如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )
如图所示,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN=4$\sqrt{3}$cm,则∠ACM的度数是( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
12.在平面直角坐标系中,点(-6,-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的正方体,得到一个如图所示的零件,则这个零件的主视图是( )
从棱长为2的正方体毛坯的一角,挖去一个棱长为1的正方体,得到一个如图所示的零件,则这个零件的主视图是( )



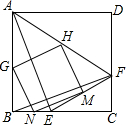 如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.
如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.