题目内容
19.抛掷三枚硬币,则出现一枚正面向上、两枚正面向下的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
分析 首先求得将一枚硬币向上连续抛掷三次共有的情况;再根据其中出现一枚正面向上、两枚正面向下的情况数,计算即可.
解答 解:画树状图得:
将一枚硬币向上连续抛掷三次,共有8种情况;
其中出现一枚正面向上、两枚正面向下有2种,所以其概率=$\frac{2}{8}$=$\frac{1}{4}$.
故选B.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
10. 在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
 在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.
在正方形上给定8个点,以这些点为顶点,能构成( )个等腰三角形.| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
9.已知(m2+n2)2-2(m2+n2)-3=0,则m2+n2=( )
| A. | -1或3 | B. | 3 | C. | -1 | D. | 无法确定 |
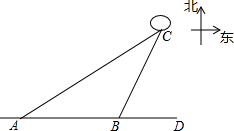 一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.
一条船从海岛A出发,以25海里/时的速度向正东方向航行,2小时后到达海岛B处,从A、B望灯塔C,测得∠DBC=68°,∠DAC=34°,求海岛B与灯塔C的距离.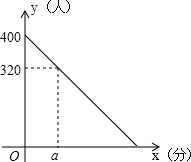 春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.
春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示. 如图,点A、B在⊙O上,点C是OB延长线上一点,∠AOB=2∠BAC.
如图,点A、B在⊙O上,点C是OB延长线上一点,∠AOB=2∠BAC.