题目内容
15．抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，5），则a-b+c的值为（ ）| A． | 0 | B． | -1 | C． | 1 | D． | 5 |
分析 由二次函数的对称性可知P点关于对称轴对称的点为P′（-1，5），故当x=-1时可求得y值为5，即可求得答案．
解答 解：
∵抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，
∴P（3，5）对称点坐标为（-1，5），
∴当x=-1时，y=5，
即a-b+c=5，
故选D．
点评 本题主要考查二次函数的性质，利用二次函数的对称性求得点（-1，5）在其图象上是解题的关键．
练习册系列答案
相关题目
10．下列说法正确的是（ ）
| A． | 单项式-$\frac{{x}^{2}}{3}$的系数是-3 | B． | 单项式2πa3的次数是4 | ||
| C． | 多项式x2y2-2x2+3是四次三项式 | D． | 多项式x2-2x+3的项分别是x2、2x、3 |
20．
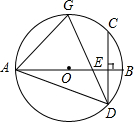如图，已知AB是⊙O的直径，弦CD⊥AB于点E，G是$\widehat{AB}$的中点，连结AD，AG，CD，则下列结论不一定成立的是（ ）
如图，已知AB是⊙O的直径，弦CD⊥AB于点E，G是$\widehat{AB}$的中点，连结AD，AG，CD，则下列结论不一定成立的是（ ）| A． | CE=DE | B． | ∠ADG=∠GAB | C． | ∠AGD=∠ADC | D． | ∠GDC=∠BAD |
7．抛物线y=-$\frac{1}{2}$x2+1的顶点坐标是（ ）
| A． | （0，1） | B． | （$\frac{1}{2}$，1） | C． | （-$\frac{1}{2}$，-1） | D． | （2，-1） |
