题目内容
20.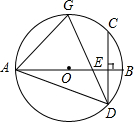 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AB}$的中点,连结AD,AG,CD,则下列结论不一定成立的是( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AB}$的中点,连结AD,AG,CD,则下列结论不一定成立的是( )| A. | CE=DE | B. | ∠ADG=∠GAB | C. | ∠AGD=∠ADC | D. | ∠GDC=∠BAD |
分析 根据圆周角定理、垂径定理以及圆心角、弧、弦的关系定理判断即可.
解答 解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE,A成立;
∵G是$\widehat{AB}$的中点,
∴$\widehat{AG}$=$\widehat{BG}$,
∴∠ADG=∠GAB,B成立;
∵AB是⊙O的直径,弦CD⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠AGD=∠ADC,C成立;
∠GDC=∠BAD不成立,D不成立,
故选:D.
点评 本题考查的是圆周角定理、垂径定理以及圆心角、弧、弦的关系,掌握相关的性质定理是解题的关键.

练习册系列答案
相关题目
10.下列说法中正确的是( )
| A. | 1的平方根和1的立方根相同 | B. | 8的立方根是±2 | ||
| C. | $\sqrt{4}$的平方根是±2 | D. | 0的平方根和0的立方根相同 |
11.在-(-2),-[-(-3)],+(-$\frac{1}{2}$),-|-2|这四个数中,负数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC.证明:
已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC.证明: 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3. 如图,△ABC的内切圆⊙O与边AB、AC分别切于点D、E,连接DE,∠ABC的平分线BF交直线DE于点F,连接CF,求证:BF⊥CF.
如图,△ABC的内切圆⊙O与边AB、AC分别切于点D、E,连接DE,∠ABC的平分线BF交直线DE于点F,连接CF,求证:BF⊥CF.