题目内容
7.抛物线y=-$\frac{1}{2}$x2+1的顶点坐标是( )| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | (-$\frac{1}{2}$,-1) | D. | (2,-1) |
分析 利用抛物线顶点坐标公式可求得答案.
解答 解:
∵-$\frac{b}{2a}$=-$\frac{0}{-2×(-\frac{1}{2})}$=0,$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{2})×1-0}{4×(-\frac{1}{2})}$=1,
∴顶点坐标为(0,1),
故选A.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点坐标公式是解题的关键.

练习册系列答案
相关题目
17.若分式$\frac{x-1}{x+1}$的值为零,则x的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
2.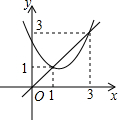 如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;
如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;
②3b+c+6=0;
③当x2+bx+c>$\frac{2}{x}$时,x>2;
④当1<x<3时,x2+(b-1)x+c<0,
其中正确的序号是( )
 如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;
如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;②3b+c+6=0;
③当x2+bx+c>$\frac{2}{x}$时,x>2;
④当1<x<3时,x2+(b-1)x+c<0,
其中正确的序号是( )
| A. | ①②④ | B. | ②③④ | C. | ②④ | D. | ③④ |
19.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次连续行驶纪录如表.(单位:km)
(1)在第五次纪录时距A地最远.
(2)求收工时距A地多远?
(3)若行驶每km耗油0.4升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +6 | -8 | +7 | +5 | -4 | -2 |
(2)求收工时距A地多远?
(3)若行驶每km耗油0.4升,问共耗油多少升?
 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3. 如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证:
如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证: 如图,在△ABC中,∠C=65°,∠ADB=85°,AD是△ABC的角平分线,求∠B的度数.
如图,在△ABC中,∠C=65°,∠ADB=85°,AD是△ABC的角平分线,求∠B的度数.