题目内容
4.已知∠MAN=120°,AC平分∠MAN,点B、D分别在射线AN、AM上.(1)如图(1),若∠ABC=∠ADC=90°,求证:①DC=BC;②AD+AB=AC.
(2)如图(2),若∠ABC+∠ADC=180°,(1)中的结论①、②是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
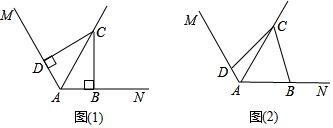
分析 (1)①根据角平分线上的点到角的两边距离相等可得DC=BC,②根据角平分线的定义求出∠BAC=∠DAC=60°,然后求出∠ACB=∠ACD=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得AB=$\frac{1}{2}$AC,AD=$\frac{1}{2}$AC,从而得证;
(2)过点C作CE⊥AB于E,作CF⊥AD于F,根据同角的补角相等求出∠ABC=∠CDF,根据角平分线上的点到角的两边距离相等可得CE=CF,然后利用“角角边”证明△BCE和△DCF全等,根据全等三角形对应边相等可得DC=BC,BE=DF,从而求出AD+AB=AE+AF,然后根据(1)的结论得证.
解答 证明:(1)①∵AC平分∠MAN,∠ABC=∠ADC=90°,
∴DC=BC,
②∵∠MAN=120°,AC平分∠MAN,
∴∠BAC=∠DAC=60°,
∵∠ABC=∠ADC=90°,
∴∠ACB=∠ACD=90°-60°=30°,
∴AB=$\frac{1}{2}$AC,AD=$\frac{1}{2}$AC,
∴AB+AD=$\frac{1}{2}$AC+$\frac{1}{2}$AC=AC,
即AD+AB=AC;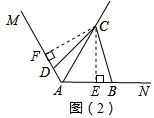
(2),(1)中的结论①、②仍然成立.
理由如下:如图,过点C作CE⊥AB于E,作CF⊥AD于F,
∵∠ABC+∠ADC=180°,
∠CDF+∠ADC=180°,
∴∠ABC=∠CDF,
∵AC平分∠MAN,CE⊥AB,CF⊥AD,
∴CE=CF,
在△BCE和△DCF中,$\left\{\begin{array}{l}{∠ABC=∠CDF}\\{∠BEC=∠DFC=90°}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF(AAS),
∴DC=BC,BE=DF,
∴AD+AB=AD+AE+BE=AD+AE+DF=AF+AE,
即AD+AB=AE+AF,
由(1)的结论可知AE+AF=AC,
即AD+AB=AC,
综上所述,(1)中的结论①、②仍然成立.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于(2)作辅助线构造出全等三角形.

 特高级教师点拨系列答案
特高级教师点拨系列答案| A. | y=2(x-1)2 | B. | y=2x2-1 | C. | y=2(x+1)2 | D. | y=2x2+1 |
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +6 | -8 | +7 | +5 | -4 | -2 |
(2)求收工时距A地多远?
(3)若行驶每km耗油0.4升,问共耗油多少升?
 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3. 如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证:
如图,点O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,连接OE.求证: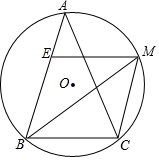 如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.
如图,在△ABC中,AB=AC,∠ABC=2∠A,BM平分∠ABC交外接圆于点M,ME∥BC交AB点E.试判断四边形EBCM的形状,并加以证明.