题目内容
心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分钟)之间满足函数解析式y=-0.1x2+2.6x+43(0≤x≤30),y值越大,表示接受能力越强.
(1)在直角坐标系中,画出该函数的图象;
(2)在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐步降低?
(3)第10分钟时,学生的接受能力是多少?
(1)在直角坐标系中,画出该函数的图象;
(2)在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐步降低?
(3)第10分钟时,学生的接受能力是多少?
考点:二次函数的应用
专题:
分析:(1)根据二次函数的解析式将其改写成顶点式的形式即可;
(2)仔细观察图象可知:当0≤x≤13时,y随x值的增大而增大,当13<x≤30时,y随x值的增大而减少;
(3)根据已知的函数关系,把x=10代入关系式求解即可;
(2)仔细观察图象可知:当0≤x≤13时,y随x值的增大而增大,当13<x≤30时,y随x值的增大而减少;
(3)根据已知的函数关系,把x=10代入关系式求解即可;
解答: 解:(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9,
解:(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9,
示意图如图(图象基本正确);
(2)当0≤x≤13时,学生的接受能力逐步增强;
当13<x≤30时,学生的接受能力逐步降低.
(3)当x=10时,y=-0.1×102+2.6×10+43=59,
则第10分钟时,学生的接受能力是59.
 解:(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9,
解:(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9,示意图如图(图象基本正确);
(2)当0≤x≤13时,学生的接受能力逐步增强;
当13<x≤30时,学生的接受能力逐步降低.
(3)当x=10时,y=-0.1×102+2.6×10+43=59,
则第10分钟时,学生的接受能力是59.
点评:本题主要考查的是二次函数在实际生活中的应用,是各地中考的热点,在解题时注意数形结合思想的运用,同学们要加强训练.属于中档题.

练习册系列答案
相关题目
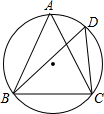 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| AC |
(1)求证:△ABC是等边三角形.
(2)过点B作BP∥CD,交DA延长线于点P,请依题意画出示意图.若AD=1,CD=5,求BD的长.
下列各图形中,其中的一个三角形是由另一个三角形通过平移得到的是( )
A、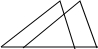 |
B、 |
C、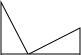 |
D、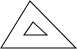 |
 如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是
如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°,则∠EDC的度数是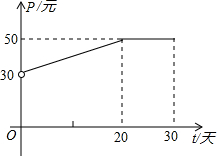 根据市场调查,某种新产品投放市场30天内,每件产品的销售价格
根据市场调查,某种新产品投放市场30天内,每件产品的销售价格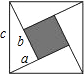 如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?
如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么? 观察如图所示的长方形.
观察如图所示的长方形.