题目内容
在△ABC中,D为BC边的中点,E为AC边上任意一点,BE交AD于点O,李瑞学生在研究这一问题时,发现了如下的事实:
(1)当
=
=
时,有
=
=
(如图1);
(2)当
=
=
时,有
=
=
(如图2);
(3)当
=
=
时,有
=
=
(如图3);
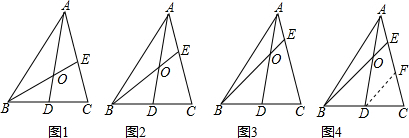
在图4中,当
=
时,参照上述研究结论,请你猜想用n表示
的一般结论 .
(1)当
| AF |
| AC |
| 1 |
| 2 |
| 1 |
| 1+1 |
| AO |
| AD |
| 2 |
| 3 |
| 2 |
| 2+1 |
(2)当
| AF |
| AC |
| 1 |
| 3 |
| 2 |
| 2+1 |
| AO |
| AD |
| 2 |
| 4 |
| 2 |
| 2+2 |
(3)当
| AF |
| AC |
| 1 |
| 4 |
| 1 |
| 1+3 |
| AO |
| AD |
| 2 |
| 5 |
| 2 |
| 2+3 |

在图4中,当
| AE |
| AC |
| 1 |
| 1+n |
| AO |
| AD |
考点:平行线分线段成比例,三角形中位线定理
专题:规律型
分析:作DF∥BE交AC于F,如图4,根据平行线分线段成比例定理,由DF∥BE得到
=
,则EF=CF,再利用比例性质由
=
得到
=
,再由OE∥DF得到
=
=
,然后根据比例性质求解.
| CF |
| EF |
| CD |
| BD |
| AE |
| AC |
| 1 |
| 1+n |
| AE |
| EF |
| 2 |
| n |
| AO |
| OD |
| AE |
| EF |
| 2 |
| n |
解答:解:作DF∥BE交AC于F,如图4,
∵DF∥BE,
∴
=
=1,
∴EF=CF,
∵
=
,
∴
=
,
∴
=
=
,
∵OE∥DF,
∴
=
=
,
∴
=
.
故答案为:
(n为正整数).
∵DF∥BE,
∴
| CF |
| EF |
| CD |
| BD |
∴EF=CF,
∵
| AE |
| AC |
| 1 |
| 1+n |
∴
| AE |
| EC |
| 1 |
| n |
∴
| AE |
| EF |
| AE | ||
|
| 2 |
| n |
∵OE∥DF,
∴
| AO |
| OD |
| AE |
| EF |
| 2 |
| n |
∴
| AO |
| AD |
| 2 |
| n+2 |
故答案为:
| 2 |
| n+2 |
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4x2-2kxy+y2为一完全平方式,则k为( )
| A、4 | B、-2 | C、±4 | D、±2 |
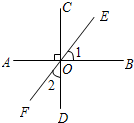 如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(
如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(| A、∠1=∠2 |
| B、∠1+∠2=90° |
| C、∠1+∠2=180° |
| D、无法确定 |
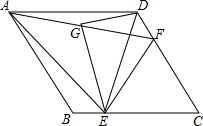 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.  如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟.
如图,点P从点A出发沿着线段AB向点B匀速运动,点P出发4分钟时距A地240cm,此时点Q也从点A沿着线段AB向点B匀速运动,再经过6分钟点Q追上点P,又经过2分钟点Q到达点B处,此时点P、Q同时停止运动,设点P的运动时间为t分钟. 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF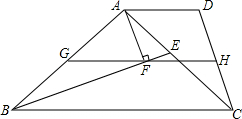 如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证:
如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证: