题目内容
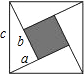 如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?
如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?考点:勾股定理的证明
专题:
分析:方法一:图中阴影部分的面积=大正方形的面积-四个小直角三角形的面积,根据正方形的面积公式和直角三角形的面积公式进行解答即可.
方法二:图中阴影部分是边长为(b-a)的正方形,其面积为(b-a)2.
方法二:图中阴影部分是边长为(b-a)的正方形,其面积为(b-a)2.
解答:解:如图,方法一:S阴影=S正方形-4S直角三角形=c2-4×
ab=c2-2ab.
方法二:图中阴影部分是边长为(b-a)的正方形,其面积为(b-a)2,
所以c2-2ab=(b-a)2,即c2-2ab=a2-2ab+b2,
所以a2+b2=c2.
| 1 |
| 2 |
方法二:图中阴影部分是边长为(b-a)的正方形,其面积为(b-a)2,
所以c2-2ab=(b-a)2,即c2-2ab=a2-2ab+b2,
所以a2+b2=c2.
点评:本题考查了勾股定理的证明.此题利用了图中阴影部分的面积不变找到等量关系的,由此列出方程c2-2ab=a2-2ab+b2,易推知a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
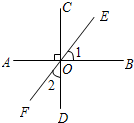 如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(
如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(| A、∠1=∠2 |
| B、∠1+∠2=90° |
| C、∠1+∠2=180° |
| D、无法确定 |
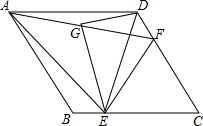 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF. 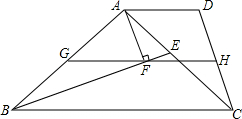 如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证:
如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证: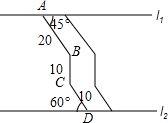 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m. 如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE为
如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°,若∠AOC=40°,则∠DOE为