题目内容
 根据市场调查,某种新产品投放市场30天内,每件产品的销售价格
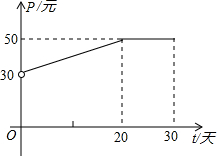
根据市场调查,某种新产品投放市场30天内,每件产品的销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间
t(天)之间的关系见表.
| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)根据表求出日销售量Q(件)与时间t(天)之间的函数关系式;(函数关系只限于一次函数、二次函数、反比例函数)
(3)在这30天内,哪一天的日销售金额最大?最大是多少元?(日销售金额=每件产品销售价格×日销售量)
考点:二次函数的应用
专题:
分析:(1)根据图象,每件销售价格P与时间t的函数关系为一次函数,用待定系数法确定函数的解析式即可;
(2)设它们所在直线l的解析式,代入计算,可得结论;
(3)利用日销售金额=每件产品销售价格×日销售量,确定分段函数,分段求出函数的最值,即可求得结论.
(2)设它们所在直线l的解析式,代入计算,可得结论;
(3)利用日销售金额=每件产品销售价格×日销售量,确定分段函数,分段求出函数的最值,即可求得结论.
解答:解:(1)根据图示,前20天该产品每件销售价格P(元)与时间t(天)的函数是一次函数,且过点(0,30),(20,50),
所以可设为y=ax+b,把(0,30),(20,50),
代入得
,
解得
.
故所求函数关系为P=t+30(0<t<20);
(2)由表1设日销售量Q(件)与时间t(天)之间的函数关系式为y=mt+n,
把(20,20),(30,10)代入得
,
解得
,
所求的解析式为Q=-t+40(0<t≤30);
(3)前20天,日销售金额=PQ=(t+30)(-t+40)=-t2+10t+1200=-(t-5)2+1225;
后10天,每件产品的销售价格50元,日销售金额=PQ=50(-t+40)=-50t+2000,(20≤t≤30),
所以当t=20时,日销售金额取得最大值,最大值等于1000元,
综上,当t=5时,即第5天时,日销售金额取得最大值,最大值等于1225元.
所以可设为y=ax+b,把(0,30),(20,50),
代入得
|
解得
|
故所求函数关系为P=t+30(0<t<20);
(2)由表1设日销售量Q(件)与时间t(天)之间的函数关系式为y=mt+n,
把(20,20),(30,10)代入得
|
解得
|
所求的解析式为Q=-t+40(0<t≤30);
(3)前20天,日销售金额=PQ=(t+30)(-t+40)=-t2+10t+1200=-(t-5)2+1225;
后10天,每件产品的销售价格50元,日销售金额=PQ=50(-t+40)=-50t+2000,(20≤t≤30),
所以当t=20时,日销售金额取得最大值,最大值等于1000元,
综上,当t=5时,即第5天时,日销售金额取得最大值,最大值等于1225元.
点评:本题考查函数解析式的确定,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
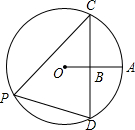 如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从3点到6点整,钟表的时针旋转的度数为( )
| A、.30° | B、60° |
| C、90° | D、120° |
 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF 如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是
如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是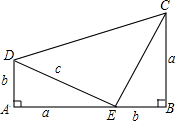 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?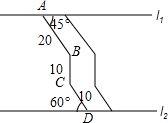 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.