题目内容
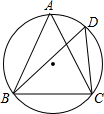 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| AC |
(1)求证:△ABC是等边三角形.
(2)过点B作BP∥CD,交DA延长线于点P,请依题意画出示意图.若AD=1,CD=5,求BD的长.
考点:圆周角定理,等边三角形的判定与性质
专题:
分析:(1)利用圆周角定理和圆周角、弧、弦的关系得到AB=AC,∠A=60°,则ABC是等边三角形.
(2)过A作BP的垂线,交BP于E,交CD的延长线于F,先证△BPD是等边三角形,得出BD=PD=BP,再求出AC,设BD=PD=BP=x,求出AP、PE、AE、BE,在Rt△ABE中,根据勾股定理AE2+BE2=AB2,即可求出x.
(2)过A作BP的垂线,交BP于E,交CD的延长线于F,先证△BPD是等边三角形,得出BD=PD=BP,再求出AC,设BD=PD=BP=x,求出AP、PE、AE、BE,在Rt△ABE中,根据勾股定理AE2+BE2=AB2,即可求出x.
解答:(1)证明:∵在⊙O中,
=
,
∴AB=AC.
又∵∠CDB=60°,∠CDB=∠A,
∴∠A=60°,
∴等腰△ABC是等边三角形.
(2)由(1)得,△ABC1是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠ADB=∠ACB=60°,∠BDC=∠BAC=60°,
∴∠ADC=60°+60°=120°,
∵BP∥CD,
∴∠P+∠ADC=180得,
∴∠P=60°,
∴∠P=∠ADB=60°,
∴BD=BP,
∴△BPD是等边三角形,
∴BD=PD=BP,
过A作BP的垂线,交BP于E,交CD的延长线于F,如图所示:
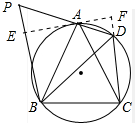 ∵BP∥CD,
∵BP∥CD,
∴∠AFD=90°,
∵∠ADF=180°-120°=60°,∠DAF=30°,
∴DF=
CD=
,AF=
,
∴CF=
,AC2=AF2+CF2=(
)2+(
)2=31,
∴AC=
,
设BD=PD=BP=x,则AP=x-1,PE=
,AE=
,BE=
,
在Rt△ABE中,AE2+BE2=AB2,
即(
)2+(
)2=(
)2,
解得x=6,或x=-5(舍去),
即BD=6.
 |
| AB |
 |
| AC |
∴AB=AC.
又∵∠CDB=60°,∠CDB=∠A,
∴∠A=60°,
∴等腰△ABC是等边三角形.
(2)由(1)得,△ABC1是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠ADB=∠ACB=60°,∠BDC=∠BAC=60°,
∴∠ADC=60°+60°=120°,
∵BP∥CD,
∴∠P+∠ADC=180得,
∴∠P=60°,
∴∠P=∠ADB=60°,
∴BD=BP,
∴△BPD是等边三角形,
∴BD=PD=BP,
过A作BP的垂线,交BP于E,交CD的延长线于F,如图所示:
 ∵BP∥CD,
∵BP∥CD,∴∠AFD=90°,
∵∠ADF=180°-120°=60°,∠DAF=30°,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴CF=
| 11 |
| 2 |
| ||
| 2 |
| 11 |
| 2 |
∴AC=
| 31 |
设BD=PD=BP=x,则AP=x-1,PE=
| x-1 |
| 2 |
| ||
| 2 |
| x+1 |
| 2 |
在Rt△ABE中,AE2+BE2=AB2,
即(
| x-1 |
| 2 |
| ||||
| 2 |
| 31 |
解得x=6,或x=-5(舍去),
即BD=6.
点评:本题考查了圆周角定理和等边三角形的判定与性质以及勾股定理的运用;通过作辅助线证明等边三角形和运用勾股定理是解决问题的关键.

练习册系列答案
相关题目
4x2-2kxy+y2为一完全平方式,则k为( )
| A、4 | B、-2 | C、±4 | D、±2 |
方程x2-3x=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定是否有实数根 |
若A是一个四次多项式,且B也是一个四次多项式,则A-B一定是( )
| A、八次多项式 |
| B、四次多项式 |
| C、三次多项式 |
| D、不高于四次的多项式或单项式 |
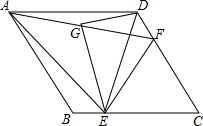 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.