题目内容
1. 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)
分析 先求出AB两点的坐标,进而可得出结论.
解答 解:∵直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,
∴A(4,0),B(0,2),
∴当点P在直线y=-$\frac{1}{2}$x+2上时,-$\frac{1}{2}$+2=m,解得m=$\frac{3}{2}$,
∵点P(1,m)在△AOB的形内,
∴0<m<$\frac{3}{2}$,
∴m的值可以是1.
故答案为:1.
点评 本题考查的是一次函数图象上点的坐标特征,熟知一次函数图象上图象上点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
6.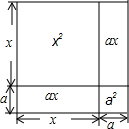 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )| A. | (x+a)(x+a) | B. | x2+a2+2ax | C. | 4(x+a) | D. | (x+a)a+(x+a)x |
13.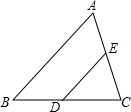 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
10.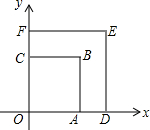 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
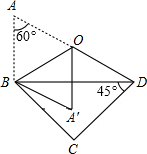 如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么?
如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么?
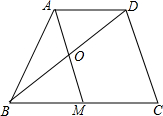 如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.
如图,在四边形ABCD中,点M是边BC的中点,AD∥BC,AM∥DC,AM与BD交于点O.求证:AO=OM.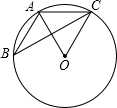 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.
如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.