题目内容
12.已知长方形纸片ABCD的长AD=8,宽AB=4,如图(1).(1)将纸片沿EF折叠后,点D,C分别落在D′,C′的位置,如图(2)所示,若∠EFB=66°,求∠AED′的度数;
(2)如图(3)所示,若点P从点C以2个单位长度/秒的速度在边CB上向点B移动,同时点Q从点B以1个单位长度/秒的速度在边BA上向点A移动,设移动的时间为t(0<t<4)秒,请问:在点P,Q移动的过程中,是否存在时间t的某一取值范围,使得S△ADQ<S△DPC?若存在,求出时间t的取值范围;若不存在,说明理由.

分析 (1)先由长方形的性质求出∠DEF=∠EFB=66°,再利用折叠的性质得出∠FEB=66°,最后利用平角的应用即可得出结论;
(2)先用t表示出△ADQ和△DPC的面积,建立不等式即可得出结论.
解答 解:(1)在长方形ABCD中,AD∥BC,
∴∠DEF=∠EFB=66°,
由折叠知,∠FED'=∠DEF=66°,
∵∠AED'+∠FED'+∠DEF=180°,
∴∠AED'=180°-(∠FED'+∠DEF)=180°-(66°+66°)=48°,
(2)由题意知,QA=4-t,CP=2t,
∵AD=8,CD=4,
∴S△ADQ=$\frac{1}{2}$AD•QA=$\frac{1}{2}$×8×QA=4(4-t),
S△DPC=$\frac{1}{2}$CD•CP=$\frac{1}{2}$×4×CP=4t,
∵S△ADQ<S△DPC,
∴4(4-t)<4t,
∴t>2,
∵0<t<4,
∴2<t<4,
即:2<t<4时,使得S△ADQ<S△DPC.
点评 此题是四边形综合题,主要考查了长方形的性质,折叠的性质,三角形的面积公式,解不等式,解(1)的关键是求出∠FED'=66°,解(2)的关键是用三角形的面积的不等关系建立不等式,是一道常规题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
7.已知一次函数y=kx+m-2x与y轴的负半轴相交,且函数值y随x增大而减小,则下列结论正确的是( )
| A. | k<2,m>0 | B. | k<2,m<0 | C. | k>2,m>0 | D. | k>2,m<0 |
17.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )
| A. | 65° | B. | 65°或115° | C. | 50° | D. | 50°或115° |
4. 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )
 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠AOF=25°,求∠CDO的度数( )| A. | 50° | B. | 45° | C. | 35° | D. | 65° |
2.方程2x-y=3和2x+y=9的公共解是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ |
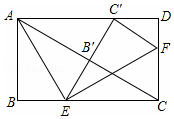 如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为2:3.
如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为2:3.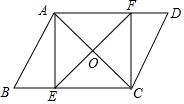 如图,在?ABCD中,AB=4cm,AD=6cm,点E、F是?ABCD边BC、AD上的两点,BE=DF,AC,EF相交于点O,若AC⊥EF,则△ABE的周长为10cm.
如图,在?ABCD中,AB=4cm,AD=6cm,点E、F是?ABCD边BC、AD上的两点,BE=DF,AC,EF相交于点O,若AC⊥EF,则△ABE的周长为10cm.