题目内容
4.心理学家发现,学生对概念的接受能力与提出概念所用的时间x(单位:分)之间满足式子-0.1x2+2.6x+43(0≤x≤30).如果使学生的接受能力达到59,用多长时间?你知道学生的最大接受能力是多少吗?分析 此题实际是求当函数值为59.9时,自变量的值.直接代入解答即可.
解答 解:把y=59.9代入y=-0.1x2+2.6x+43中得:
x1=x2=13分钟,
即学生对概念的接受能力达到59.9需要13分钟.
点评 本题考查了二次函数的最值、一元二次方程的应用,解题时,把实际问题转化为数学问题,就是已知函数值,求自变量的值,得出题目的结论.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9. 如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
 如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.
如图EF∥GF∥IJ∥BC,共有( )对相似的三角形.| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
10.若△ABC的三边a,b,c满足a2+b2-8a-10b+29+|c-3|=0,则( )
| A. | △ABC是直角三角形且∠C=90° | B. | △ABC是锐角三角形 | ||
| C. | △ABC是直角三角形且∠B=90° | D. | △ABC是直角三角形且∠A=90° |
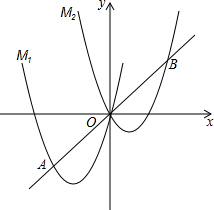 如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1