题目内容
15．
如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B=75°，∠C=45°，求∠DAE的度数．
分析 由三角形的内角和定理，可求∠BAC=60°，又由AE是∠BAC的平分线，可求∠BAE=30°，再由AD是BC边上的高，可求得∠BAD=15°，所以∠DAE=∠BAE-∠BAD=15°．
解答 解：在△ABC中，∠B=75°，∠C=45°，
∴∠BAC=180°-∠B-∠C=60°，
∵AE是∠BAC的平分线，
∴∠BAE=∠CAE=30°．
又∵AD是BC边上的高，
∴∠ADB=90°，
∵在△ABD中，∠BAD=90°-∠B=15°，
∴∠DAE=∠BAE-∠BAD=15°．
点评 本题主要考查三角形的内角和定理及角平分线的性质，高线的性质，解答的关键是掌握三角形的内角和等于180°．
练习册系列答案
阅读快车系列答案
相关题目
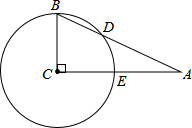如图，在△ABC中，∠C=90°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E．
如图，在锐角三角形ABC中，sinB=$\frac{3}{5}$，tanC=3，且S△ABC=20，求BC的长．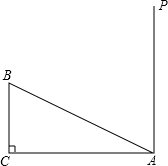
如图，在Rt△ABC中，∠C=90°，AC=16，BC=8，MN=AB，点M、N分别在AC和过点A且垂直于AC的射线AP上运动，问：点M运动到什么位置时，△ABC和以A、M、N为顶点的三角形全等（画出图形，写出解答过程）．