题目内容
5. 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.(1)求证:四边形DEFG是平行四边形;
(2)如果△ABC中AB=AC,四边形DEFG的形状是矩形(直接写出结果).
分析 (1)利用三角形中位线定理推知ED∥FG,ED=FG,则由“对边平行且相等的四边形是平行四边形”证得四边形DEFG是平行四边形;
(2)矩形.连接AO并延长交BC于点M,先由三角形中线的性质得出M为BC的中点,当AB=AC时,由等腰三角形三线合一的性质得出AM⊥BC,再由三角形中位线的性质及平行线的性质得出EF⊥FG,从而证明四边形EFGH是矩形.
解答 解:(1)∵D、E分别为AC、AB的中点
∴ED∥BC,ED=$\frac{1}{2}$BC.
同理FG∥BC,FG=$\frac{1}{2}$BC,
∴ED∥FG,ED=FG,
∴四边形DEFG是平行四边形.
(2)如图1,当AB=AC时,?DEFG变成矩形.
理由如下:
连接AO并延长交BC于点M.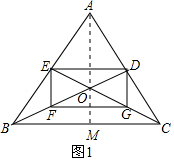
∵三角形的三条中线相交于同一点,△ABC的中线BD、CE交于点O,
∴M为BC的中点,
当AB=AC时,AM⊥BC,
∵E,F,G分别是AB,OB,OC的中点,
∴EF∥AO,FG∥BC,
∴EF⊥FG;
∴四边形EFGH是矩形.
故答案为:矩形.
点评 本题考查了平行四边形、矩形的判定,三角形的中位线性质定理,三角形中线的性质及等腰三角形的性质,其中三角形的中位线的性质定理为证明线段相等和平行提供了依据.

练习册系列答案
相关题目
15. 如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
 如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )| A. | 60° | B. | 55° | C. | 45° | D. | 不能确定 |
 十二边形的内角和是1800°.
十二边形的内角和是1800°.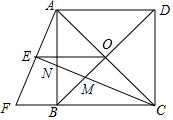 如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.
如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.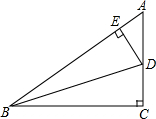 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则: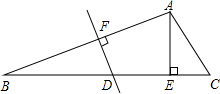 如图,在△ABC中,∠B=30°,∠C=45°,AB的垂直平分线交BC于点D,BD=6$\sqrt{2}$,AE⊥BC于点E,求CE的长.
如图,在△ABC中,∠B=30°,∠C=45°,AB的垂直平分线交BC于点D,BD=6$\sqrt{2}$,AE⊥BC于点E,求CE的长.