题目内容
14.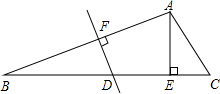 如图,在△ABC中,∠B=30°,∠C=45°,AB的垂直平分线交BC于点D,BD=6$\sqrt{2}$,AE⊥BC于点E,求CE的长.
如图,在△ABC中,∠B=30°,∠C=45°,AB的垂直平分线交BC于点D,BD=6$\sqrt{2}$,AE⊥BC于点E,求CE的长.
分析 首先作出辅助线连接AD,再利用线段垂直平分线的性质计算.
解答 解:连接AD,
∵AB的垂直平分线交BC于点D,
∴BD=AD=6$\sqrt{2}$,∴∠DAB=∠B=30°,
∴∠ADE=60°,
∵AE⊥BC,
∴AE=3$\sqrt{6}$,
∵∠C=45°,
∴EC=AE=3$\sqrt{6}$.
点评 本题考查了线段垂直平分线的性质,解直角三角形,本题关键是作出辅助线提示:连接AD.考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)有关知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
4.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.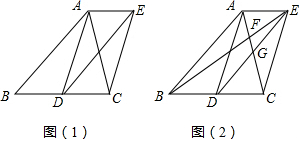

 如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.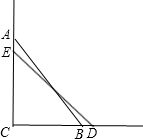 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆下端B距C点的距离为15m,当端点B向右移动5m时到达D点,而A到达E点,求滑杆顶端A下滑多少米?
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆下端B距C点的距离为15m,当端点B向右移动5m时到达D点,而A到达E点,求滑杆顶端A下滑多少米?