题目内容
16.使$\frac{\sqrt{3x+2}}{2-|x|}$有意义的x的取值范围是x≥-$\frac{2}{3}$且x≠2.分析 直接利用二次根式的定义结合分式的性质分析得出答案.
解答 解:∵$\frac{\sqrt{3x+2}}{2-|x|}$有意义,
∴3x+2≥0,2-|x|≠0,
解得:x≥-$\frac{2}{3}$且x≠2.
故答案为:x≥-$\frac{2}{3}$且x≠2.
点评 此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.

练习册系列答案
相关题目
6.下列二次根式中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{18}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
7.下列语句:①$\sqrt{16}$的算术平方根是2;②$\sqrt{(-2)^{2}}$=±2;③-3是9的平方根;④$\root{3}{8}$=$\sqrt{4}$;⑤负数没有立方根,其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.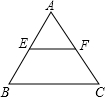 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )| A. | 15米 | B. | 20米 | C. | 25米 | D. | 30米 |
1.下列汽车标志中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点. 如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.