题目内容
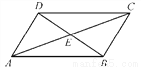
如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD＝90°，BC＝4，BE＝ED＝3，AC＝10，则四边形ABCD的面积为( )
A. 6 B. 12 C. 20 D. 24
D
【解析】试题分析：在Rt△CBE中，由勾股定理可求得EC=5，又因AC=10，所以AE=EC=5.根据对角线互相平分的四边形是平行四边形可判定四边形ABCD是平行四边形，所以平行四边形ABCD的面积为BC×BD=4×6=24，故答案选D.
不等式﹣2x＜4的解集是（ ）
A. x＞2 B. x＜2 C. x＜﹣2 D. x＞﹣2
D
【解析】两边同时除以﹣2，得：x＞﹣2．
故选D． 如图，点A，B为定点，定直线l//AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：
①线段MN的长；
②△PAB的周长；
③△PMN的面积；
④直线MN，AB之间的距离；
⑤∠APB的大小．
其中会随点P的移动而变化的是（ ）
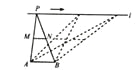
A. ②③ B. ②⑤ C. ①③④ D. ④⑤
B
【解析】试题分析：
①、MN=AB，所以MN的长度不变；
②、周长C△PAB=（AB+PA+PB），变化；
③、面积S△PMN=S△PAB=×AB·h，其中h为直线l与AB之间的距离，不变;
④、直线NM与AB之间的距离等于直线l与AB之间的距离的一半，所以不变；
⑤、画出几个具体位置，观察图形，可知∠APB的大小在变化。
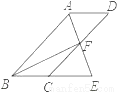
故选：B 如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．
（1）求证：BE=CD；
（2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．
（1）详见解析；（2）.
【解析】试题分析：（1）由平行四边形的性质和角平分线易证∠BAE=∠BEA，根据等腰三角形的性质可得AB=BE；（2）易证△ABE是等边三角形，根据等边三角形的性质可得AE=AB=4，AF=EF=2，由勾股定理求出BF，再由AAS证明△ADF≌△ECF，即△ADF的面积=△ECF的面积，因此平行四边形ABCD的面积=△ABE的面积=AE•BF，即可得出结果．
... 如图，在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3.若平行四边形ABCD的周长是16，则EC的长为________．
2
【解析】试题分析：由平行四边形的性质和已知条件证出∠BAE=∠BEA，证出AB=BE=3；求出AB+BC=8，得出BC=5，即可得出EC的长．∵四边形ABCD是平行四边形，∴AD∥BC，AB=CD，AD=BC，∴∠AEB=∠DAE，
∵平行四边形ABCD的周长是16，∴AB+BC=8，∵AE是∠BAD的平分线，∴∠BAE=∠DAE，
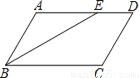
∴∠BAE=∠AEB，∴AB=BE=3，∴... 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）
A. 150° B. 130° C. 120° D. 100°
C
【解析】试题分析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABE，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，∵∠BED=150°，∴∠ABE=∠AEB=30°，∴∠A=180°﹣∠ABE﹣∠AEB=120°．故选C． 如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．
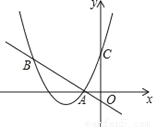
（1）抛物线解析式为y=x2+4x+3，一次函数解析式为y=﹣x﹣1；（2）由图象可知，满足（x+2）2+m≥kx+b的x的取值范围为x?﹣4或x≥﹣1．
【解析】（1）先利用待定系数法先求出m，再求出点B坐标，利用方程组求出太阳还是解析式．
（2）根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围．
【解析】
（1）∵抛物线y=（x+2）2+m经过点A（﹣1，0... 已知二次函数y=﹣2x2+4x﹣3，如果y随x的增大而减小，那么x的取值范围是（ ）
A. x≥1 B. x≥0 C. x≥﹣1 D. x≥﹣2
A
【解析】【解析】
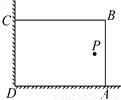
∵y=﹣2x2+4x﹣3=﹣2（x﹣1）2﹣1，∴抛物线开口向下，对称轴为x=1，∴当x≥1时，y随x的增大而减小．故选A． 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边)，设AB＝xm.
(1)若花园的面积为192m2，求x的值；
(2)若在P处有一棵树与墙CD、AD的距离分别是13m和6m，要将这棵树围在花园内(含边界，不考虑树的粗细)，求花园面积S的最大值．
(1)12或16(2)当x＝13时，S最大＝195
【解析】试题分析：（1）根据题意得出长×宽=192，进而得出答案；
（2）由在P处有一棵树与墙CD，AD的距离分别是13m和6m，求出x的取值范围，根据二次的性质求解即可.
试题解析：(1)(28－x)x＝192，解得x1＝12，x2＝16，
∴x的值为12或16.
(2)∵S＝x(28－x)＝－x2＋28x(6≤x≤1...