Question

2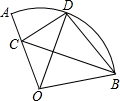．如图，在扇形AOB中，∠AOB=100°，半径OA=9，将扇形OAB沿着过点B的直线折叠，点O恰好落在弧AB上的点D处，折痕交OA于点C，则弧AD的长等于2π．

Answer 1

分析 先证明△ODB是等边三角形，得到∠DOB=60°，根据弧长公式即可解决问题．

解答 解：∵△BCD是由△BCO翻折得到，
∴∠CBD=∠CBO，∠BOD=∠BDO，
∵OD=OB，
∴∠ODB=∠OBD，
∴∠ODB=2∠DBC，
∵∠ODB+∠DBC=90°，
∴∠ODB=60°，∵OD=OB
∴△ODB是等边三角形，
∴∠DOB=60°，
∵∠AOB=100°，
∴∠AOD=∠AOB-∠DOB=40°，
∴弧AD的长=$\frac{40•π•9}{180}$=2π，
故答案为2π．

点评 本题考查翻折变换、弧长公式、等边三角形的判定和性质等知识，解题的关键是等边三角形的发现，属于中考常考题型．