题目内容
12.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-5)=0的根,则这个三角形的周长为( )| A. | 12 | B. | 15 | C. | 12或15 | D. | 以上都不对 |
分析 先利用因式分解法解方程得到x1=2,x2=5,再根据三角形三边的关系得到x=5,然后计算三角形的周长.
解答 解:x-2=0或x-5=0,
所以x1=2,x2=5,
因为2+4=6,
所以第三边长为5,
所以三角形的周长为4+6+5=15.
故选B.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了三角形三边的关系.

练习册系列答案
相关题目
4.将抛物线y=2x2经过怎样的平移可得到抛物线y=2(x+3)2-4( )
| A. | 先向左平移3个单位,再向上平移4个单位 | |
| B. | 先向左平移3个单位,再向下平移4个单位 | |
| C. | 先向右平移3个单位,再向上平移4个单位 | |
| D. | 先向右平移3个单位,再向下平移4个单位 |
1.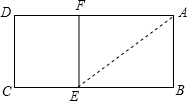 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | 4 | D. | 2$\sqrt{3}$ |
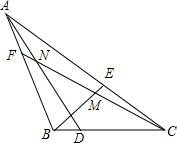 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).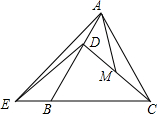 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.

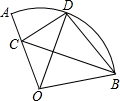 如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π.
如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π.