题目内容
12.解下列方程.(1)$\frac{5x-4}{x-2}$=$\frac{4x+10}{3x-6}$-1
(2)$\frac{3}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:15x-12=4x+10-3x+6,
移项合并得:14x=28,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:3x-3+2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若(ambn)3=a9b15,则m,n的值分别为( )
| A. | m=9;n=5 | B. | m=3;n=5 | C. | m=5;n=3 | D. | m=6;n=12 |
7.抛物线y=-5x2-x+9与y轴的交点坐标为( )
| A. | (9,0) | B. | (-9,0) | C. | (0,-9) | D. | (0,9) |
4.$\sqrt{100}$的结果是( )
| A. | ±10 | B. | $\sqrt{10}$ | C. | -10 | D. | 10 |
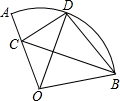 如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π.
如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π. 小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜.
小明家有一块三角形菜地,要种面积相等的四种蔬菜,请你设计两种方案,把这块地分成四块面积相等的三角形地块分别种植这四种蔬菜.