题目内容
10.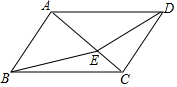 如图,在?ABCD中,AB=3,AC=4,BC=5,AE=2CE,求四边形BCDE的面积.
如图,在?ABCD中,AB=3,AC=4,BC=5,AE=2CE,求四边形BCDE的面积.
分析 由勾股定理的逆定理易证△BAC是直角三角形,再由条件AE=2CE可求出CE的长,进而可求出△BEC的面积,则四边形BCDE的面积为△BEC面积的2倍,问题得解.
解答 解:
∵AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴△BAC是直角三角形,
∴∠BAC=90°,
即BA⊥AC,
∵AE=2CE,AC=4,
∴CE=$\frac{1}{3}$AC=$\frac{4}{3}$,
∴△BEC的面积=$\frac{1}{2}$CE•AB=2,
∴四边形BCDE的面积=2S△BEC=4.
点评 本题考查了平行四边形的性质、勾股定理的逆定理运用以及三角形面积公式的运用,判断△BAC是直角三角形是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
15.方程组$\left\{\begin{array}{l}{{x}^{2}-4x+2y=-5}\\{kx-y+2=0}\end{array}\right.$ 无实数解,则k的取值范围为-1<k<5.
2.二次函数y=-3x2+6x变形为y=a(x+m)2+n形式,正确的是( )
| A. | y=-3(x+1)2-3 | B. | y=-3(x-1)2-3 | C. | y=-3(x+1)2+3 | D. | y=-3(x-1)2+3 |
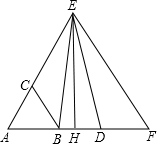 如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由.
如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由.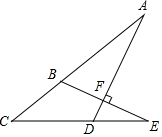 如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°.
如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°.